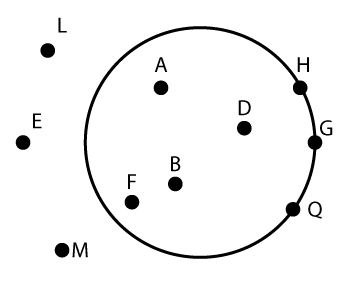
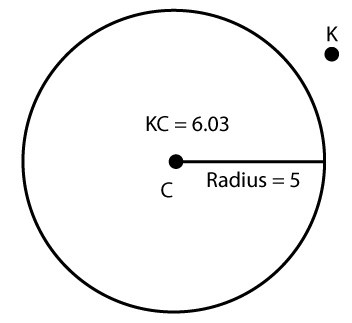
If we are going to work with inscribed and circumscribed objects (and we are), then we will need to be able to tell the difference between points that are inside a circle, outside a circle, and on a circle.
This may seem simple enough, but let's review. Click on each tab to review what it means to be inside a circle, on a circle, and outside a circle.
Inside the Circle
On the Circle
Outside the Circle
What does it mean to be inside a circle?
Simple Definition
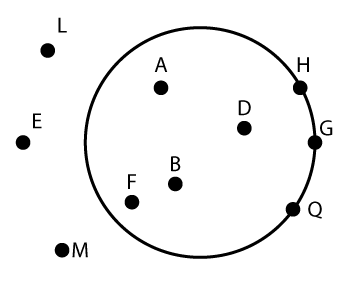
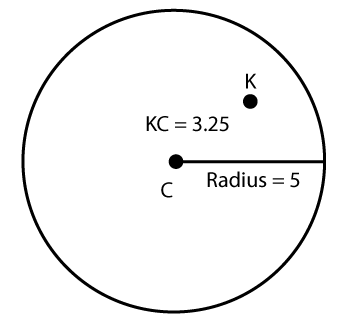
A point is inside a circle if it lies within the interior of the circle.
More Technical Definition
If the distance between a point and a circle's center is less than the length of the radius, then that point is inside the circle.
Click on the images to find out which points are inside the circle.
What does it mean to be on the circle?
Simple Definition
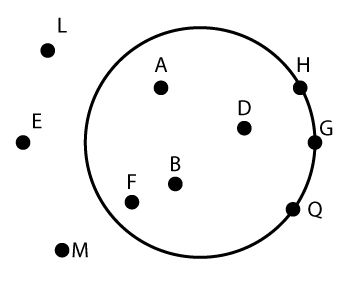
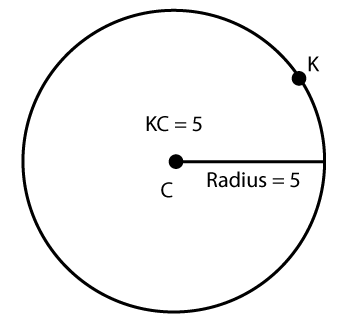
A point is on the circle if it is actually on the circle's edge.
More Technical Definition
A point is on the circle if the distance between the point and a circle's center is exactly equal to the length of the radius.
Click on the images to find out which points are on the circle.
What does it mean to be outside the circle?
Simple Definition
If a point is not on the interior or edge of a circle, then the point is outside the circle.
More Technical Definition
A point is outside a circle if the distance between the point and a circle's center is greater than the length of the circle's radius.
Click on the images to find out which points are outside the circle.
Now, it's your turn. In the matching activity below, match each point to its position relative to the circle.
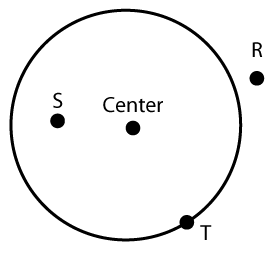
|
Point R
Point S
Point T
|
On the Circle
Outside the Circle
Inside the Circle
|