You have a pretty good understanding of inside, outside, and on a circle. Let's take it a step further and look at some figures that are inside a circle. Click through the slide show below to take a closer look at inscribed angles and their properties.

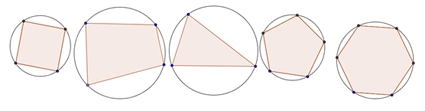
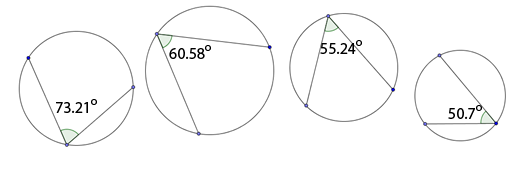
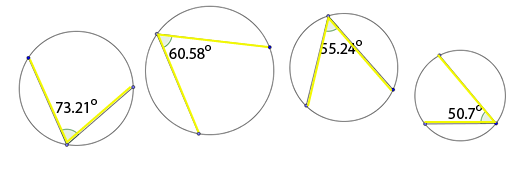
Look at this group of polygons that are inside circles. Besides having a similar color, what is something that they all seem to have in common? Each vertex of an inscribed polygon appears to lie on the circle. With the exception of the vertices, the polygon lies inside the circle. Now, take a look at these angles that are inscribed. How is an inscribed angle like an inscribed polygon? Each vertex lies on the circle. There is only one vertex for each inscribed angle. Each of the inscribed angles also appears to be formed by a special type of circle segment. What type of special line segments form the inscribed angles? Each angle is formed by two chords of a circle. Chords are line segments that have endpoints that lie on a circle. The segment intersects a circle at exactly two points, which happen to be the segment's endpoints and form the angle's vertex.

Based on what you have discovered about inscribed angles, how would you define an inscribed angle? Click below to see if your definition is close to ours.