As you saw in the video, the Inscribed Angle Theorem is a pretty powerful theorem relating the measure of an inscribed angle to the measure of the corresponding intercepted arc. Now, let's see this theorem at work on some more problems. Click on the tabs below to work through some example problems.
Problem 1
Problem 2
Problem 3
Problem 4
Take a look at the figure below.
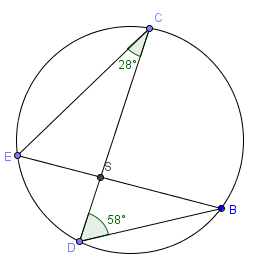
What is the measure of \(\small\mathsf{ \overset{\displaystyle\frown}{ED} }\)?
Look at the table below for the steps to solve this problem.
| Identify any inscribed angles with known angle measures. | ∠C is an inscribed angle with a known angle measure of 28°. ∠D is an inscribed angle with a known angle measure of 58°. |
| Do the sides of one of these angles happen to intercept \(\small\mathsf{ \overset{\displaystyle\frown}{ED} }\)? | ∠C sides intercept \(\small\mathsf{ \overset{\displaystyle\frown}{ED} }\). |
| Now, we can use the Inscribed Angle Theorem to find the arc's measure. Apply the Inscribed Angle Theorem and a little algebra. | ∠C measure should be \(\mathsf{ \frac{1}{2} }\) the measure of its intercept arc, \(\small\mathsf{ \overset{\displaystyle\frown}{ED} }\). So 28 is half of what number? Let's let n represent that number: \(\mathsf{ 28 = \frac{1}{2}n }\) \(\mathsf{ 2 \cdot 28 = 2 \cdot \frac{1}{2}n }\) 56 = n |
So the measure of \(\small\mathsf{ \overset{\displaystyle\frown}{ED} }\) is 56°.

| What's the measure of \(\small\mathsf{ \overset{\displaystyle\frown}{CB} }\)? | By the Inscribed Angle Theorem, ∠D is \(\mathsf{ \frac{1}{2} }\) the measure of \(\small\mathsf{ \overset{\displaystyle\frown}{CB} }\). The measure of ∠CB = 58°, which would make \(\small\mathsf{ \overset{\displaystyle\frown}{CB} }\) equal to twice that, or 116°. |
| What is the measure of ∠E? | ∠E has an intercepted arc that's \(\small\mathsf{ \overset{\displaystyle\frown}{CB} }\). From earlier application of the Inscribed Angle theorem, we know that the measure of \(\small\mathsf{ \overset{\displaystyle\frown}{CB} }\) is 116°. That would mean the ∠E's measure is \(\mathsf{ \frac{1}{2} }\) of 116°, or 58°. |
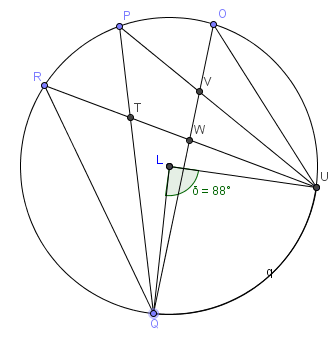
What are the measures of ∠R, ∠P, and ∠O?
All three of these angles share the same intercepted arc, \(\small\mathsf{ \overset{\displaystyle\frown}{QU} }\), which has a measure of 88°. From the Inscribed Angle Theorem, this means that ∠R, ∠P, and ∠O will each be half of 88°. So m∠R =m∠P = m∠O = 44°.
What is the value of y in the figure below?
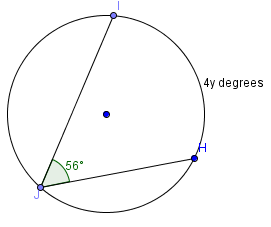
How can you find the value of y?
We know that the measure of \(\small\mathsf{ \overset{\displaystyle\frown}{HI} }\) should be equal to twice the measure of the associated inscribed angle ∠J, which is 56°. So the measure of \(\small\mathsf{ \overset{\displaystyle\frown}{HI} }\) is 112°.
With the help of a little algebra, we can solve for y.
\(\mathsf{ 4y = 2 \cdot 56 = 112 }\)
\(\mathsf{ 4y = 112 }\)
\(\mathsf{ \frac{4y}{4} = \frac{112}{4} }\)
\(\mathsf{ y = 28 }\)
