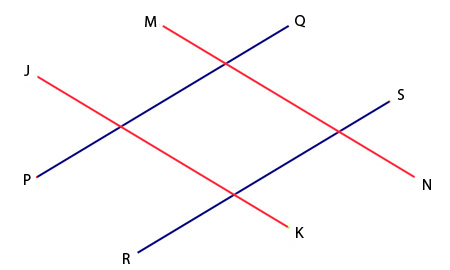
Let's look at another example of a parallelogram that is part of a larger, more complex shape. What are the vertices of the parallelogram in this figure? When you've found the parallelogram, click the image to check your answer.
Question
Given the definition of a parallelogram, what do you know about the relationships among segments AB, CD, AD, and BC?
Opposite sides of a parallelogram are congruent. Hence, AB = CD and AD = BC.
The sides, interior angles, and exterior angles of the parallelogram have special names, and they have special relationships to each other. Use the slides below to learn more about the sides and angles of the parallelogram.
|
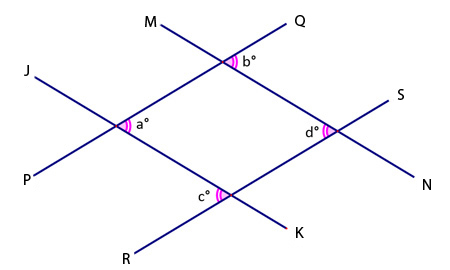
Any parallelogram has two sets of parallel lines and two sets of transversal lines. (Remember that a transversal is any line that intersects two or more lines.) In this case, lines PQ and RS are parallel to each other with transversal lines JK and MN. Similarly, lines JK and MN are parallel to each other with transversal lines PQ and RS.
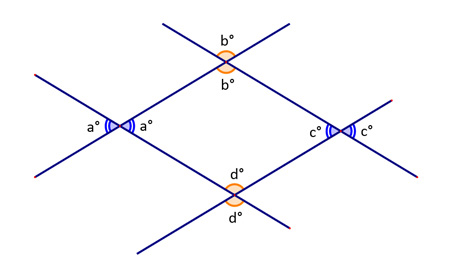
The parallel and transversal lines form several angles that have special relationships to other. Each interior angle in the parallelogram has a corresponding vertical angle. Vertical angles are created opposite each other whenever two lines cross. For example, the two angles labeled a° are vertical to each other. Vertical angles are congruent. Angles b° and d° are also opposite interior angles. In mathematical terms, a° = c° and b° = d°.
The parallel and transversal lines form alternate interior angles.When two parallel lines are cut by a transversal, the angles opposite the transversal and inside the parallel lines are alternate interior angles. For example, angles a° and c° are alternate interior angles of parallel lines PQ and RS. Angles b° and c° are also alternate interior angles of lines PQ and RS. What do you know to be true about alternate interior angles? Alternate interior angles are congruent.There are also corresponding angles in this figure. When two parallel lines are cut by a transversal, the corresponding angles are on the same side of the transversal and on the same sides of the parallel lines. Here, angles c° and d° are corresponding angles of parallel lines JK and MN. Angles a° and b° are also corresponding angles of lines JK and PQ. Like alternate interior angles, corresponding angles are congruent.
When two parallel lines are cut by a transversal, as in a parallelogram, the opposite angles on either side of the transversal and outside the parallel lines are alternate exterior angles. For instance, angles a° and d° are alternate exterior angles of parallel lines PQ and RS. Also, angles b° and c° are alternate exterior angles of parallel lines JK and MN. Alternate exterior angles are congruent. |
Because it is formed by parallel lines that are cut by a transversal, every parallelogram demonstrates properties of these lines. You should be able to identify these properties after studying the slides above.
| Properties of Parallel Lines Cut by a Transversal |
| 1. Vertical angles are congruent. |
| 2. Alternate interior angles are congruent. |
| 3. Adjacent interior angles are supplementary. |
| 4. Corresponding angles are congruent. |
| 5. Alternate exterior angles are congruent. |