If you understand the relationships among parallelogram parts, including which angles are congruent and which are supplementary, you can figure out other details about a parallelogram, given a partial set of measurements. Work through the problems below to see how it's done. If you don't answer all of the questions correctly, work through the problems again.
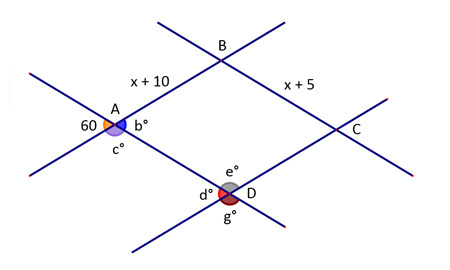
1. Which angle is vertical to the 60° angle?
That's right, this is a vertical angle to the 60° angle marked.
Think about the definition of vertical angles.
Think about the definition of vertical angles.
2. What is the measure of e°?
Angles b° and e° are supplementary. First find b° and then solve for e°.
That's right! Angles b° and e° are supplementary. First find b° and then solve for e°.
Angles b° and e° are supplementary. First find b° and then solve for e°.
3. What is the measure of d°?
Yes! Angles d° and b° are alternate interior angles and are therefore congruent. If you find b°, then you know d°.
Angles d° and b° are alternate interior angles and are therefore congruent. If you find b°, then you know d°.
Angles d° and b° are alternate interior angles and are therefore congruent. If you find b°, then you know d°.
4. The length of segment AB = x + 10 cm and segment BC = x + 5 cm. If the perimeter of parallelogram ABCD is 46 cm, what is x?
The perimeter is the sum of all the sides, and opposite sides of a parallelogram are congruent. Add the sides and use algebra to solve for x.
The perimeter is the sum of all the sides, and opposite sides of a parallelogram are congruent. Add the sides and use algebra to solve for x.
The perimeter is the sum of all the sides, and opposite sides of a parallelogram are congruent. Add the sides and use algebra to solve for x.
You got # out of # correct. Click the Retry button for another attempt.
You got a perfect score. Great job!
