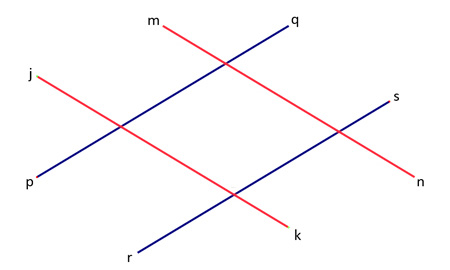
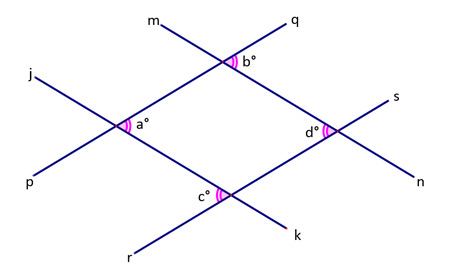
Any time you encounter a parallelogram in a problem, you'll need to recall its many special angles, and the ways in which they relate to each other. (Some are congruent, and others are supplementary.) Use the activity below to practice that skill—name the sides and angles of each parallelogram.
Click here to begin.
Lines mn and jk are
|
|
transversal
perpendicular
parallel
|
|
Think about the origin of the word parallelogram.
Think about the origin of the word parallelogram.
|
Line jk is to lines pq and rs.
|
|
parallel
transversal
perpendicular
|
|
Think about the term for a line that intersects two other lines.
Think about the term for a line that intersects two other lines.
|
If parallel lines jk and mn are cut by transversal pq, then a° and b° are angles.
|
|
corresponding
alternate exterior
alternate interior
|
|
Which type of angles are on the same side of the transversal and the same side of the parallel lines?
Which type of angles are on the same side of the transversal and the same side of the parallel lines?
|
If parallel lines pq and rs are cut by transversal jk, then a° and c° areangles.
|
|
corresponding
alternate exterior
alternate interior
|
|
What type of angles are on alternate sides of the transversal and inside the parallel lines?
What type of angles are on alternate sides of the transversal and inside the parallel lines?
|
Complete