Review what you've learned about the angles and sides of parallelograms before your quiz on this lesson. Can you identify various angles, solve algebraic problems with the sides, write proofs to show congruency, and use midpoints to construct parallelograms? If so, apply your knowledge to answer these multiple choice questions.
Which of the following quadrilaterals is NOT a parallelogram?
- rectangle
- square
- rhombus
- trapezoid
Which shape does not have all the properties of a parallelogram?
Which shape does not have all the properties of a parallelogram?
Which shape does not have all the properties of a parallelogram?
That's correct.
In the figure below, what is the measure of angle e°?
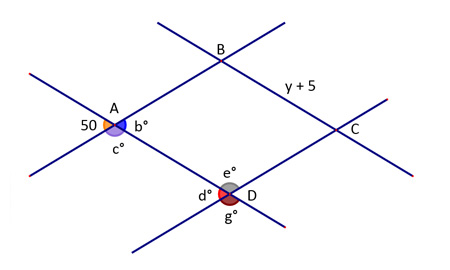
- 50°
- 130°
- 180°
- 90°
Angles b° and e° are supplementary. First find b° and then use the definition of supplementary to calculate e°.
Angles b° and e° are supplementary. First find b° and then use the definition of supplementary to calculate e°.
Angles b° and e° are supplementary. First find b° and then use the definition of supplementary to calculate e°.
Angles b° and e° are supplementary. First find b° and then use the definition of supplementary to calculate e°.
Parallelogram ABCD is a square with a perimeter of 60. What is the measure of \(\small\mathsf{ \overline{AB} }\)?
- 60
- 40
- 15
- 10
Since the parallelogram is a square, all sides have equal length, and the perimeter is the sum of all the sides.
Since the parallelogram is a square, all sides have equal length, and the perimeter is the sum of all the sides.
Since the parallelogram is a square, all sides have equal length, and the perimeter is the sum of all the sides.
Since the parallelogram is a square, all sides have equal length, and the perimeter is the sum of all the sides.
When using a quadrilateral to construct a parallelogram, which of the following statements is FALSE?
- Opposite sides and angles of the quadrilateral must be congruent.
- The midpoints of each side must be connected.
- The angles do not have to be congruent.
- The sides do not have to be congruent.
That's correct.
Review the steps for constructing a parallelogram.
Review the steps for constructing a parallelogram.
Review the steps for constructing a parallelogram.
Summary
Questions answered correctly:
Questions answered incorrectly:
