Let's Break it Down
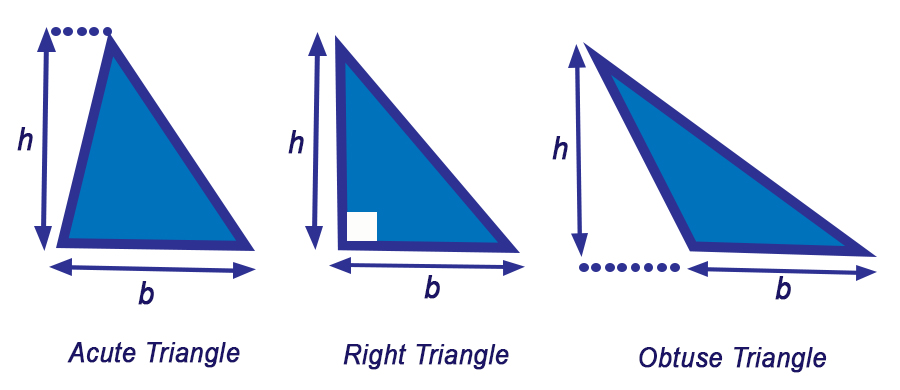
While the perimeter is the distance around the figure, the area is the amount of space inside the figure.
When you consider the square lawns and triangular flower beds that you maintain as part of your business, the area is the total amount of space covered by the square or triangle. Look at the shading in each image to see what this means. The shading on the lawn shows the area of the lawn, and the shading on the garden shows the area of the garden.
Imagine that you were mowing the square-shaped lawn.
The area is the entire space you would mow.
Imagine that you were cultivating the plants in the triangle-shaped garden bed.
All the plants within the bed make up the area.
You can calculate the area of the square lawns that you'll mow and the area of the triangular garden beds you will trim. Click each tab to learn how to calculate the area of each shape.
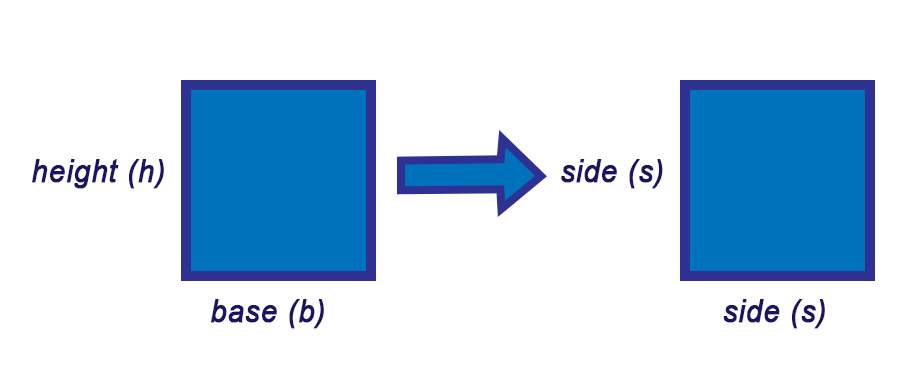
Consider a square with height (h) and base (b). The area (A) of that square is the product of the base and height.
\(A = (b)(h)\)
However, since all sides of a square are the same, the base and height are equal. Therefore, you don't have to differentiate between the base and height. Instead, you can write them both as side (s).
\(A = (s)(s)\)
When you simplify the equation above, you see that the area of a square is the square of one of the sides.
\(A = s^2\)
If a square has a side \(s = 4 \text{km}\), then what is the area of the square?
\(A = s^2 =(4 \text{km})^2 = 16 \text{km}^2\)
Just as with squares, when calculating the area of a triangle, you need to identify the base (b) and height (h). However, unlike the square, the base and height of the triangle can have different measures.
Triangles can be right, acute, or obtuse as shown. For each type of triangle below, notice how the base (b) and height (h) are identified.
In all cases, the area is half the product of the base \((b)\) and the height \((h)\).
Area of a Triangle
\(A = \frac{1}{2} (\text{base})(\text{height}) = \frac{1}{2} bh\)
If an obtuse triangle has a base \(b = 4\) km and height \(h = 6\) km, then what is the area of the triangle?
\( A = \frac{1}{2}bh = \frac{1}{2}(4 \text{ km})(6 \text{ km}) = 12\text{ km}^2 \)
Give it a shot!
Practice calculating the area of squares and triangles by completing the activity below. Answer each question, then click the question to check your answer
\(A = \frac{1}{2}bh = \frac{1}{2}(2\ \text{in}.)(10\ \text{in}.) = 10\ \text{in}.^2\) |
|
\(A = \frac{1}{2} bh = \frac{1}{2}(6\ \text{in}.)(6\ \text{in}.) = 18\ \text{in}.^2\) |
|
\(A = \frac{1}{2}bh = \frac{1}{2}(8\ \text{in}.)(4\ \text{in}.) = 16\ \text{in}.^2\) |
|
\(A = s^2 = (8\ \text{in}.)^2 = 64\ \text{in}.^2\) |
|
\(A = s^2 = (6\ \text{in}.)^2 = 36\ \text{in}.^2\) |
