Practice calculating the perimeter and area of squares and triangles in the coordinate plane by completing the activity below. Answer the question on each tab, and then check your answer.
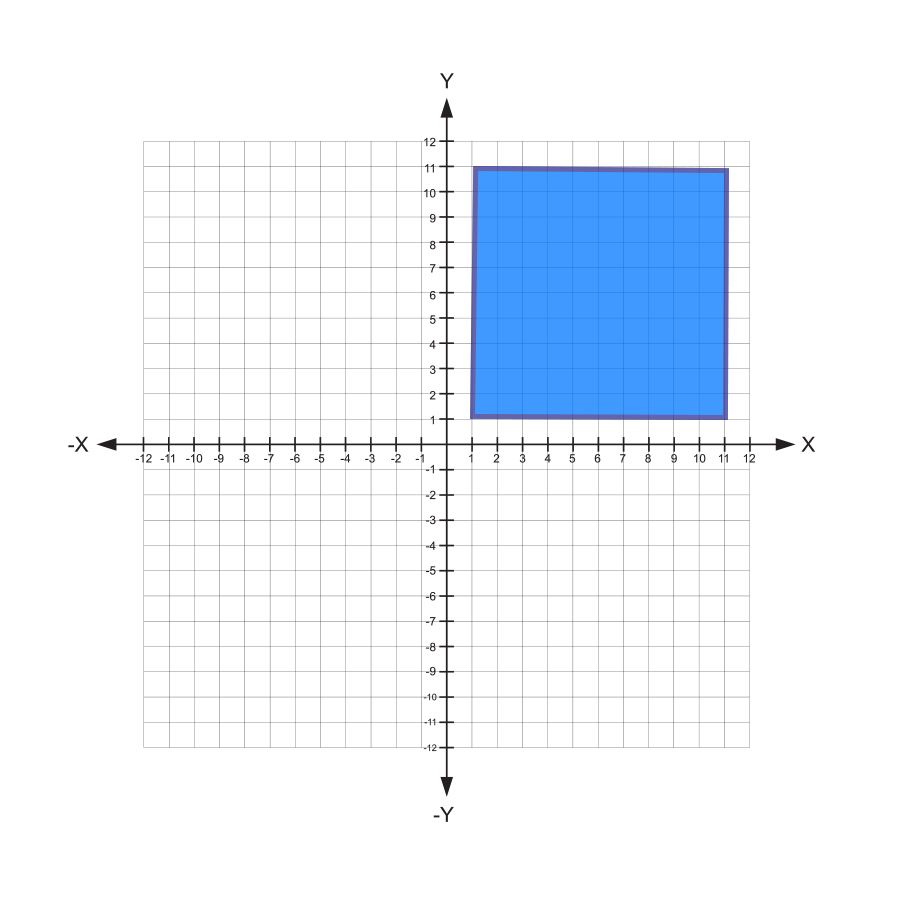
Use the coordinate plane to find the length of each side of the square and find the square’s perimeter.
The length of each side of the square is 10 units. Therefore, the perimeter is
\(P = (4)(10\ \text{units}) = 40\ \text{units}\)

For the right triangle above, the length of the longest side is 13.6 units. Use the coordinate plane to find the height, base, and perimeter of the triangle.
You can count the grid marks to determine that the height is 8 units and the base is 11 units.
Then calculate the perimeter by adding all three sides.
\(P = 13.6\ \text{units} + 11\ \text{units} + 8\ \text{units} = 32.6\ \text{units}\)

Using the coordinate plane, find the area of the square.
The length of each side is 4 units. Hence, the area of the square is
\(A = (4\ \text{units})^2 = 16\ \text{units}^2\)
