Loading...

How well do you understand the concepts and skills introduced in this lesson?

Are you ready to take this lesson's quiz? The questions below will help you find out. Make sure you understand why each correct answer is correct—if you don't, review that part of the lesson.

The length of one side of a square is 5 ft. What is the perimeter of the square?

  1. \(25\ \text{ft}^2\)

  2. \(10\ \text{ft}\)

  3. \(5\ \text{ft}\)

To calculate the perimeter of a shape, find the sum of the sides. This is actually the area of the square since \((5\ \text{ft})^2 = 25\ \text{ft}^2\).

To calculate the perimeter of a shape, find the sum of the lengths of the sides. The perimeter is \((4)(5\ \text{ft}) = 20\ \text{ft}\).

To calculate the perimeter of a shape, find the sum of the lengths of the sides. Only two sides of the square are added in this calculation.

To calculate the perimeter of a shape, find the sum of the lengths of the sides. Only a single side of the square is considered in this calculation.

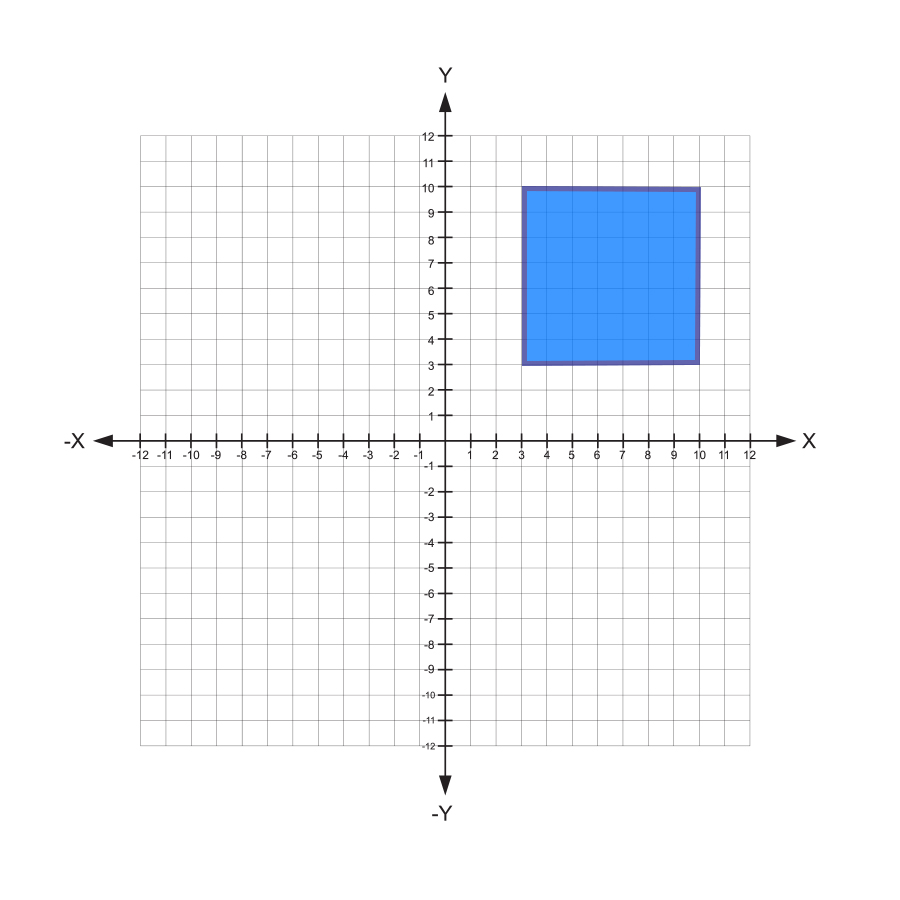
What is the perimeter of the square below?

Square on the coordinate plane with vertices at: (3,10) (10,10) (3,3) and (10,3).

  1. \(7\ \text{units}\)

  2. \(49\ \text{units}^2\)

  3. \(14\ \text{units}^2\)

By counting the grid marks, you see that the length of each side is 7. However, the perimeter is the sum of all four sides.

By counting the grid marks, you see that length of each side is 7. However, this answer choice is actually the area of the square since area \(= (7)(7) = 49 \text {units}^2\).

By counting the grid marks, you see that the length of each side is 7, and the perimeter is \((4)(7) = 28\) units.

By counting the grid marks, you see that the length of each side is 7, but this calculation only includes two sides.

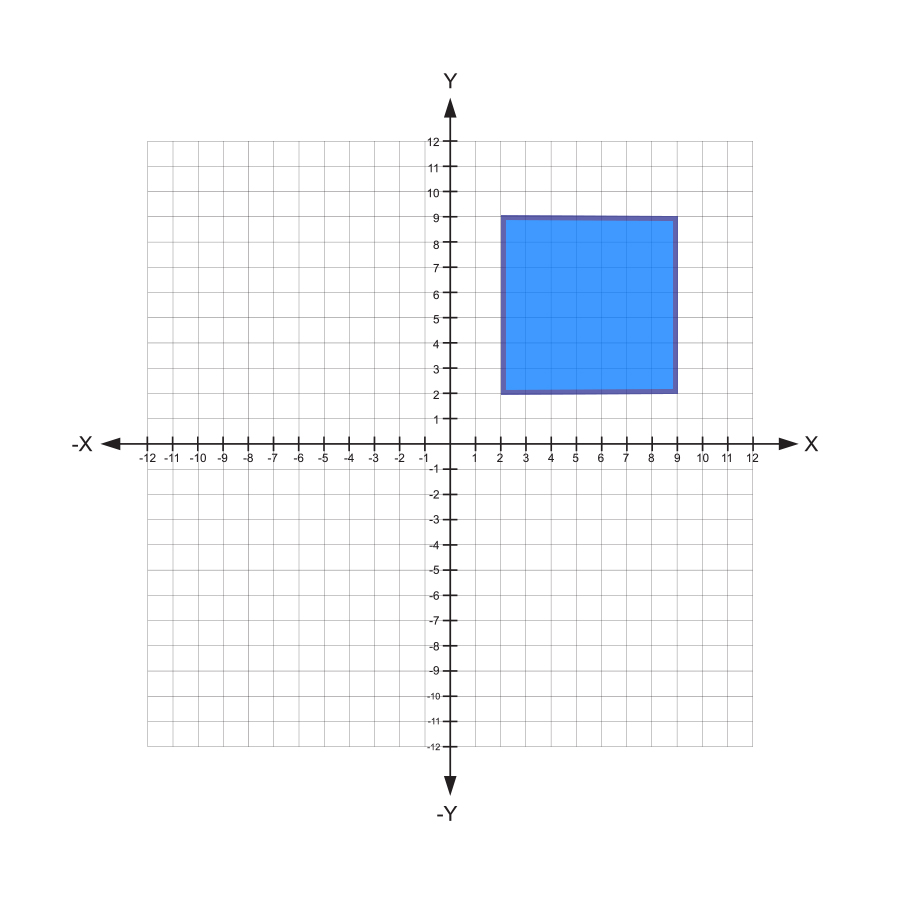
What is the area of the square below?

Square on the coordinate plane with vertices at: (2,9) (9,9) (2,2) and (9,2).

  1. \(7\ \text{units}^2\)

  2. \(24\ \text{units}^2\)

  3. \(21\ \text{units}^2\)

By counting the grid marks, you see that the length of each side is 7, and the area is \((7)(7) = 49\).

By counting the grid marks, you see that the length of each side is 7, but 7 is not the area of the square.

By counting the grid marks, you see that the length of each side is 7. Therefore, the perimeter is 24, but not the area.

By counting the grid marks, you see that the length of each side is 7, but the area is calculated by taking the square of the side length.

The sides of a triangle are 3, 4, and 5 units long. What is the perimeter of the triangle?

  1. \(8\ \text{units}\)

  2. \(9\ \text{units}\)

  3. \(25\ \text{units}\)

The perimeter is the sum of the sides, which is \(3 + 4 + 5 = 12\)

This calculation only includes the sides that are 3 and 5 units long.

This calculation only includes the sides that are 4 and 5 units long.

This calculation takes the square of the longest side, but this is not how to calculate the perimeter of a triangle.

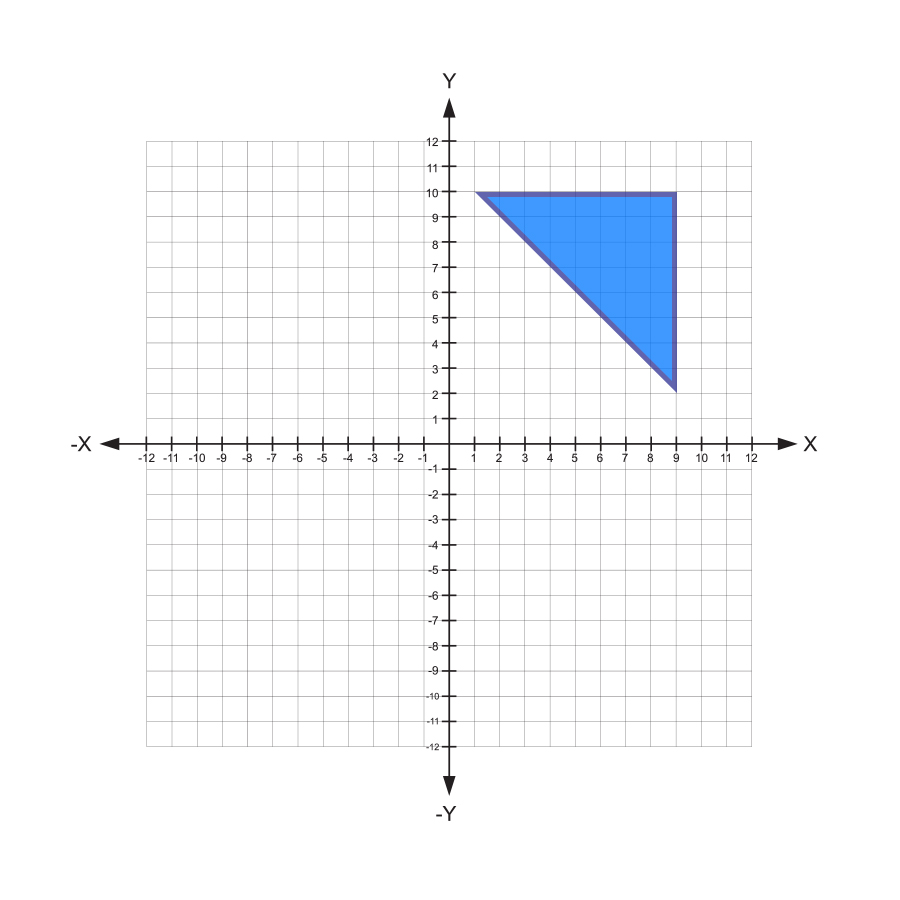
What is the area of the triangle below?

Triangle on the coordinate plane with vertices at: (9,10) (9,2) and (1,10).

  1. \(8\ \text{units}^2\)

  2. \(16\ \text{units}^2\)

  3. \(64\ \text{units}^2\)

By counting the grid marks in the coordinate plane, we see that the base is 8 and the height is 8. However, the area is half the product of the base and height.

By counting the grid marks in the coordinate plane, we see that the base is 8 and the height is 8. However, the area is not calculated by adding the base and the height.

By counting the grid marks in the coordinate plane, we see that the base is 8 and the height is 8. However, the area is half the product of the base and height.

By counting the grid marks in the coordinate plane, we see that the base is 8 and the height is 8. Therefore, the area is \((\frac{1}{2})(8)(8) = 32\ \text{units}^2\).

Summary

Questions answered correctly:

Questions answered incorrectly: