Thus far in Evan's story, Detective Reese has proven that opposite angles in a parallelogram are congruent. Use the steps demonstrated by Reese to create your own proof.
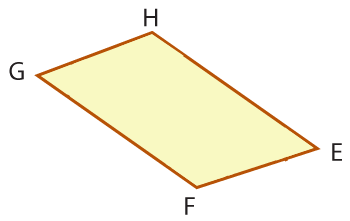
Prove that ∠F ≅ ∠H.
Create your proof by placing the following steps in the correct order.
|
Draw diagonal EG to create
△EFG and △EHG.
By SSS, △EFG ≅ △EHG.
In parallelogram EFGH, prove
∠F ≅ ∠H.
By the definition of a
parallelogram, EF
≅ HG
and FG ≅ EH. Also, FH
≅ FH by
the Reflexive Property of
Congruence.
By CPCTC, ∠F ≅ ∠H.
|
1
2
3
4
5
|
You just proved that opposite angles in a parallelogram are congruent.
