Evan was having fun with his detective story. He wanted his main character, Detective Reese, to teach the reader several facts about parallelograms, and he wrote more...
Now that Detective Reese could name the opposite angles, adjacent angles, and diagonals of a parallelogram, he wanted to use this evidence to build a case that proved certain facts about parallelograms. Reese examined the example parallelograms in the tabs below.
Example 1
Example 2
Example 3
Opposite angles of a parallelogram have a special relationship. Look at the opposite angles in ABCD.
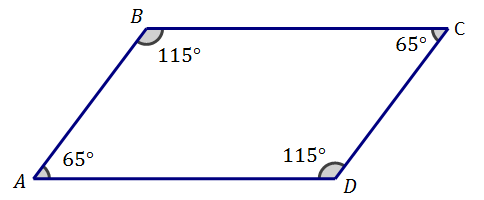
| What is the relationship between ∠A and ∠C? | The angles are congruent. |
| What is the relationship between ∠B and ∠D? | The angles are congruent. |
Adjacent angles of a parallelogram have a special relationship. Look at the adjacent angles in ABCD.

| What is the relationship between ∠A and ∠B? | The angles are supplementary. |
| What is the relationship between ∠B and ∠C? | The angles are supplementary. |
Diagonals in a special parallelogram—the rectangle—have a special relationship.
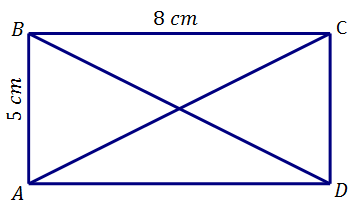
| Using the Pythagorean theorem, what is the length of diagonal AC? | AC =√82+52 = 9.4 |
| What is the length of diagonal BD? | BD = √82+52 = 9.4 |
| What is the relationship between diagonals AC and BD? | The diagonals are congruent. |
Based on the examples above, Detective Reese could build a solid case. He recorded the following three parallelogram postulates:
Parallelogram Postulates
- Opposite angles are congruent.
- Adjacent angles are supplementary.
- Diagonals in a rectangle are congruent.
Question
List three postulates that describe the angles and diagonals in a parallelogram.
