Now that Detective Reese understood how to prove if statements, he was ready to prove that a parallelogram is a rectangle if and only if its diagonals are congruent. Reese knew he had to prove these two statements:
- If a parallelogram is a rectangle, then the diagonals are congruent.
- If a parallelogram has congruent diagonals, then its a rectangle.
Read tabs 1 and 2 to see how Reese proved each statement. Then, go to the matching activity below to create your own proof.
Proof 1
Proof 2
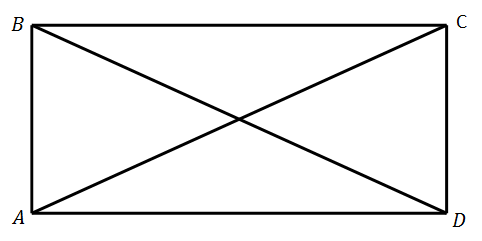
Given: Parallelogram ABCD is a rectangle.
Prove: AC = BD.
Proof
| Consider triangles △BAD and △CDA. |
| Opposite sides of a rectangle are congruent. Therefore, by definition of rectangle, AB = CD. |
| By the definition of identity, AD = AD. |
| All vertices of a rectangle are right angles. Therefore, by definition of rectangle, ∠BAD = ∠CDA. |
| By side-angle-side (SAS), △BAD \(\mathsf{ \cong }\) △CDA. |
| By CPCTC, AC = BD. |
Given: AC = BD.
Prove: Parallelogram ABCD is a rectangle.
Proof
| Consider triangles △ABD and △ADC. |
| By definition of parallelogram, AB = CD. |
| By the definition of identity, AD = AD. |
| By the given information, AC = BD. |
| By side-side-side (SSS), △ABD \(\mathsf{ \cong }\) △ADC |
| By CPCTC, ∠BAD = ∠ADC. |
| By definition of parallelogram, ∠BAD and ∠ADC are also supplementary. |
| Therefore, ∠BAD = ∠ADC = 90° because they are equal and supplementary. |
| Now consider triangles △ABC and △DCB. |
| By SSS, △ABC \(\mathsf{ \cong }\) △DCB. |
| By definitions of congruent triangles and parallelogram, ∠ABC = ∠DCB = 90° because they are equal and supplementary. |
| Hence, parallelogram ABCD has four right angles. |
| Therefore, ABCD is a rectangle. |
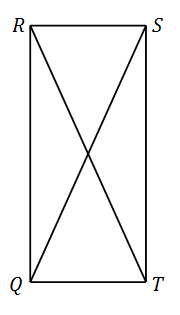
Parallelogram QRST is a rectangle. Prove QS = RT by matching the statements below to the correct reasons for each statement.
|
QR = ST
QT = QT
∠RQT = ∠STQ
△RQT ≅ △STQ
QS = RT
|
Opposite sides of a rectangle are congruent.
By SAS.
All vertices of a rectangle are right angles.
By CPCTC.
Identity
|
Good job, you got them all correct!
The answers with checkmarks are correct. Fix any answers without checkmarks and try again.
