Next, Detective Reese needed to prove that adjacent angles in a parallelogram are supplementary. Read his proof in the slide show below.
|
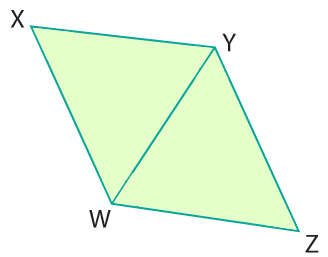
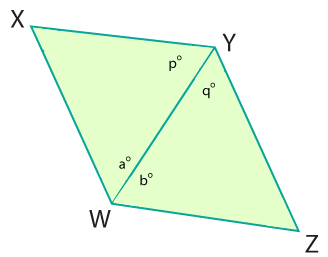
In parallelogram WXYZ, prove ∠X is supplementary to ∠W.
Draw diagonal WY to create △WXY and △WZY.
Let ∠W = ∠b° + ∠a° and let ∠Y = ∠p° + ∠q°. You know that ∠p° = ∠b° because they are alternate interior angles of parallel lines XY and WZ cut by transversal WY.
The sum of the interior angles of a triangle equals 180°. Therefore, in △WXY ∠X + ∠p° + ∠a° = 180°. Since ∠p° = ∠b°, substitute to get Since ∠W = ∠b° + ∠a°, substitute to get Hence, by the definition of supplementary, ∠X is supplementary to ∠W. |
Detective Reese was now convinced that adjacent angles in a parallelogram are supplementary.
Question
In parallelogram ABCD, angle A is opposite angle C and adjacent to angle B. Which angle is supplementary to angle A?