At this point, the detective was concerned that the parallelogram postulates could be circumstantial evidence. In other words, the postulates were true for a few specific parallelograms, but did they hold true in general? Because he was an excellent detective, Reese knew he needed proof. First, he wanted to prove that opposite angles in a parallelogram are congruent. To do so, he used the steps listed in the table below. Click each step in the table to examine the proof.

	In parallelogram EFGH, prove ∠E \(\mathsf{ \cong }\) ∠G.
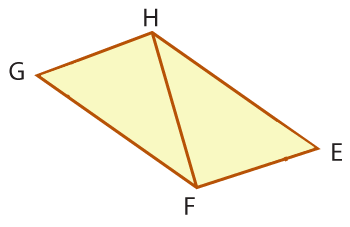	Draw diagonal FH to create △EFH and △FHG.
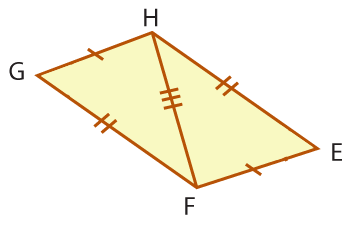	By the definition of a parallelogram, EF \(\mathsf{ \cong }\) HG and FG \(\mathsf{ \cong }\) EH. Also, FH \(\mathsf{ \cong }\) FH by the Reflexive Property of Congruence. By SSS, △EFH \(\mathsf{ \cong }\) △FHG.
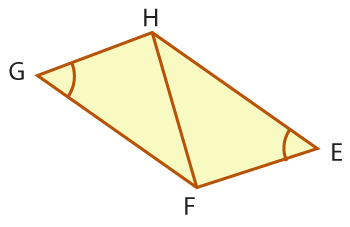	By CPCTC, ∠E \(\mathsf{ \cong }\) ∠G.

Detective Reese was now convinced that opposite angles in a parallelogram are congruent.