Processing math: 100%
Loading...

Here is one more practice problem to solve.

Graph this system of linear inequalities. Shade in the correct areas.

3y < x + 6
2y < 6x + 7

Click through the slideshow to reveal the answer steps.

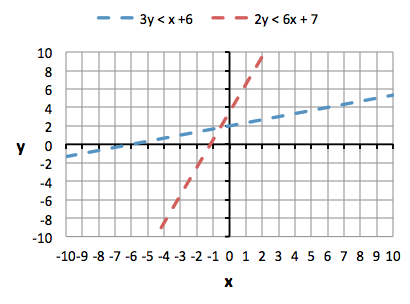
First rearrange both equations into slope-intercept form:

3y < x + 6
33y < 13x + 63
y < 13x + 2

2y < 6x + 7
22y < 62x + 72
y < 3x + 72

Draw the lines.Both lines will be dotted, and we will shade below both lines, since both equations are "less than" (<).

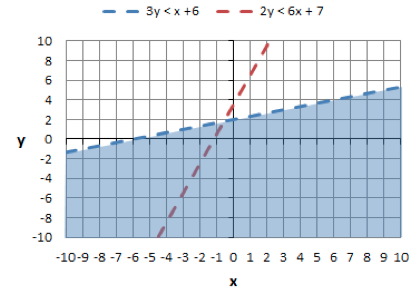
Now shade in the area below equation 1 because it is less than. (<) Here is the graph with just the shading for equation 1.

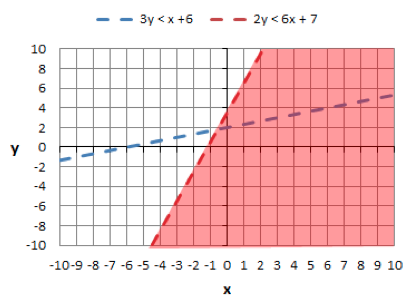
Now shade in the area below equation 2 becuase it is less than. (<) Here is the graph with just the shading for equation 2.

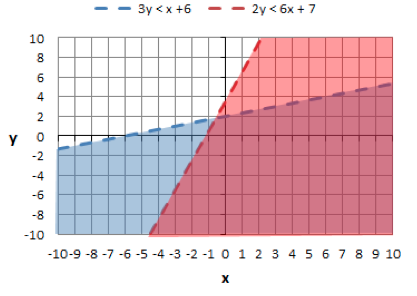
Here is the graph with shading for both equations:

Now, choose a point in the overlapping shaded area to check your answer. Let's go with (0,0). If we shaded the graph correctly, the solution should be true for both equations.

3y < x + 6
3(0) < 0 + 6
0 < 6
True		 2y < 6x + 7
2(0) < 6(0) + 7
0 < 7
True

This shows that the inequality is correctly shaded. You can also check by choosing another point outside any shaded area and the solution should be false for both equations.