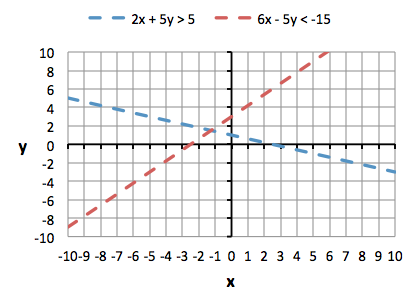
Graph this system of linear inequalities. Shade in the correct areas.
 |
2x + 5y > 5 6x - 5y < -15 |
 |
Click through the slideshow to reveal the answer steps.
|
First rearrange both equations into slope-intercept form: 2x + 5y > 5 Draw the lines. Both lines will be dotted, and we will shade above both lines, since both equations are just " greater than" (>), not greater than or equal to ≥.
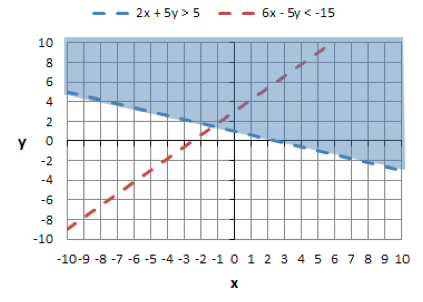
Now shade in the area above equation 1 because it is greater than 5. Here is the graph with just the shading for equation 1.
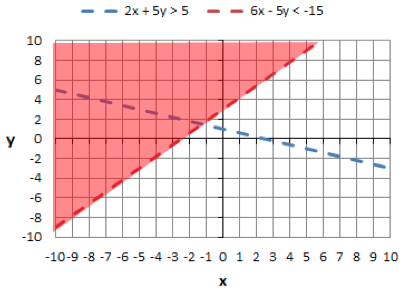
Now shade in the area above -15. Here is the graph with just the shading for equations 2.
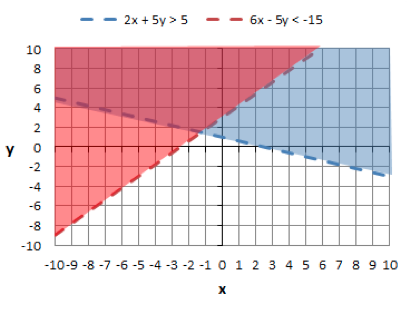
Here is the graph with shading for both equations:
Now, choose a point in the overlapping shaded area to check your answer. Let's go with (1,10).
Now, choose a point NOT in the overlapping shaded area to check your answer. Let's try (0,0) since it is not shaded at all.
|