Before you take a scored quiz for this lesson, try this set of practice questions. How well you score on this self-check will be similar to your scored quiz. If you do not score well on this self-check, please review this lesson and try again.
Which of the following system of linear inequalities is represented by the graph below?
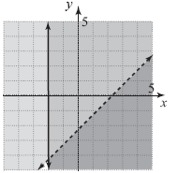
5x + y > -7
2x + 1 ≥ -4
-3x + y > - 6
x ≥ 2
-3x + 3y < -6
x ≥ -2
-2x + y ≥ -6
x ≥ -5
Dotted lines on a graph indicate less/greater than. So, one of the inequalities has an equal sign and the other does not. Also, the vertical line passes through the x-axis at -2.
Dotted lines on a graph indicate less/greater than. So, one of the inequalities has an equal sign and the other does not. Also, the vertical line passes through the x-axis at -2.
Dotted lines on a graph indicate less/greater than. So, one of the inequalities has an equal sign and the other does not. Also, the vertical line passes through the x-axis at -2.
Dotted lines on a graph indicate less/greater than. So, one of the inequalities has an equal sign and the other does not. Also, the vertical line passes through the x-axis at -2.
Give a solution to the system of linear inequalities below.
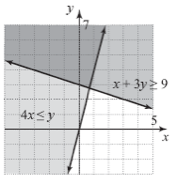
- (0,0)
- (1,3)
- (-1,-1)
- (-2,5)
Identify a point where both lines intersect. This is the dark grey area of the graph.
Identify a point where both lines intersect. This is the dark grey area of the graph.
Identify a point where both lines intersect. This is the dark grey area of the graph.
Identify a point where both lines intersect. This is the dark grey area of the graph.
What is true about the graph below?
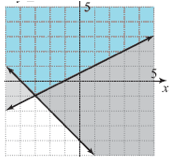
- Both linear inequalities are greater than or equal to.
- Both linear inequalities are less than or equal to.
- Both linear inequalities are greater than.
- Both linear inequalities are less than.
Both lines are solid so the both linear inequalities are solid lines.
Both lines are solid so the both linear inequalities are solid lines.
Both lines are solid so the both linear inequalities are solid lines.
Both lines are solid so the both linear inequalities are solid lines.
Which of the following is NOT a solution to the system of inequalities?
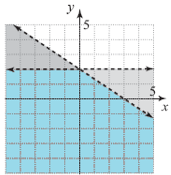
- (0, -3)
- (-1, 1)
- (0, 3)
- (-4,-4)
The solution occurs in the shaded region of the graph.
The solution occurs in the shaded region of the graph.
The solution occurs in the shaded region of the graph.
The solution occurs in the shaded region of the graph.
Summary
Questions answered correctly:
Questions answered incorrectly:
Review: Graphing One Linear Inequality
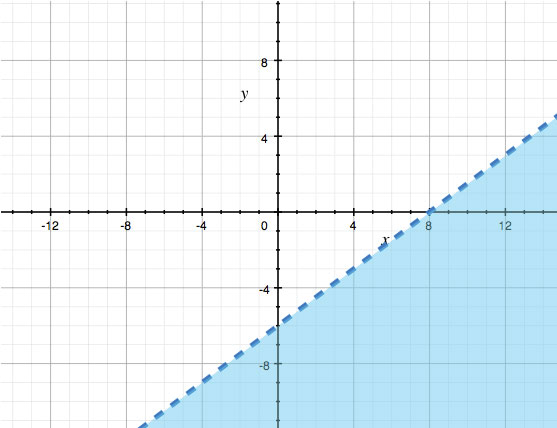
See if you can graph the inequality: y < \(\small\mathsf{ \frac{3}{4} }\)x - 6
First graph the line. Make the line dotted because the inequality is less than (<) which means that the points on the line are included in the solution.
Note: If the inequality had an equal sign (\(\small\mathsf{ \leq }\) or \(\small\mathsf{ \geq }\)), you would need a solid line.
Next, shade below the line because the values need to fall in the region less than (<) \(\small\mathsf{ \frac{3}{4} }\)x - 6 which is to the right side of the line.
Note: If the inequality were greater than (>), then you would shade above the line.
Review: Graphing One Linear Inequality
Question
Graph: 4y \(\small\mathsf{ \geq }\) 2x - 1
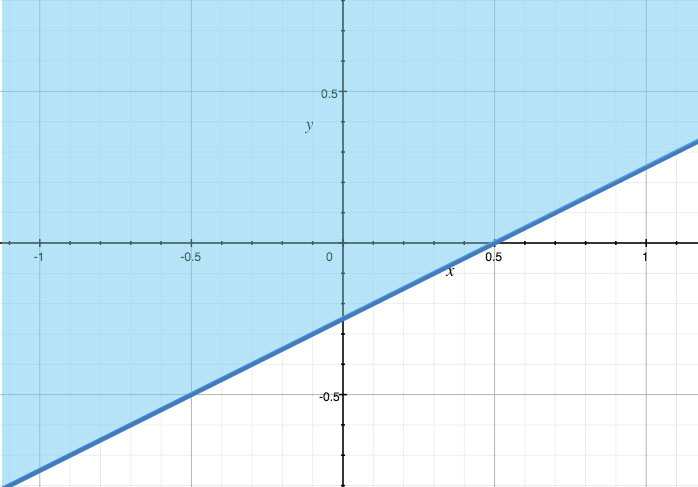
The graph would be a solid line because the inquality has an equals sign in it. Also, the shaded region should be above the line because the inquality was \(\small\mathsf{ \geq }\).
Graphing Systems of Linear Inequalities
Graphing systems of linear inequalities is just like graphing 1 linear inequality. Remember how to read the inequality sign because it affects the look of the graph.
Dotted vs. Solid Lines
If the inequality sign does NOT have an equal sign, we use a dotted line to show that the values on the actual line are not included in the solution.
If the inequality sign has an equal sign, we use a solid line to show that the values on the actual line are included in the solution.
Shading Above or Below the Line
If the inequality sign is greater than (>) or greater than or equal to (\(\small\mathsf{ \geq }\)), we shade above the line.
If the inequality sign is less than (<) or less than or equal to (\(\small\mathsf{ \leq }\)), we shade below the line.
Graphing Systems of Linear Inequalities
Study how the following problem is solved:
 |
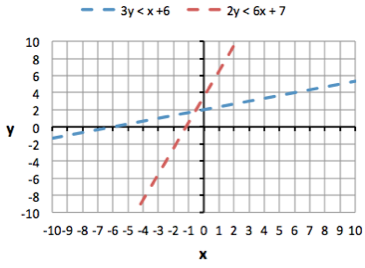
3y < x + 6 |
| 2y < 6x + 7 |
|
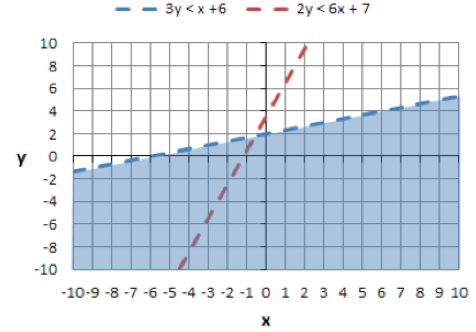
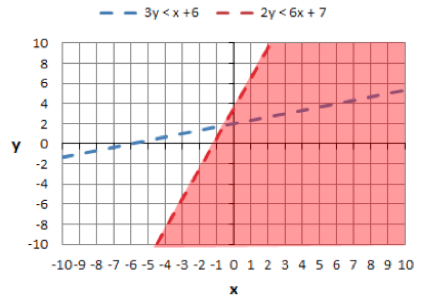
First rearrange both equations into slope-intercept form: 2y <6x + 7 Next, draw the lines. Both lines will be dotted since both equations have inequalities without equal signs.
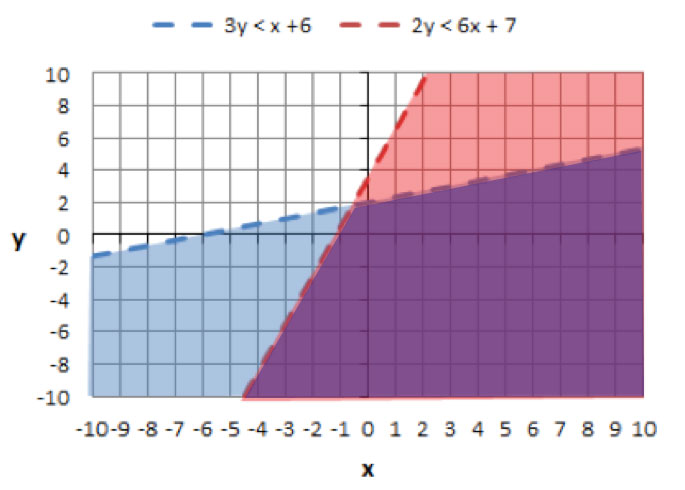
Next, we will shade below both lines, since both inequalities are "less than" (<).
The solution will be all points in the area where the lines overlap (darker pink area):
|
 |
Try This Problem
See if you can solve this problem. Click to the next screen to get started.
|
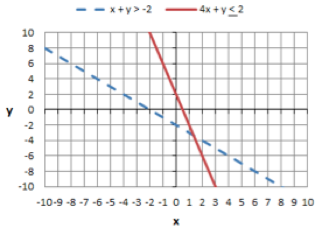
x + y > -2 |
| 4x + y \(\small\mathsf{ \leq }\) 2 |
Draw the Lines for the Graphs of This System
First, draw the lines for the graphs.
Use a dotted line for x + y > -2 because x + y is greater than, but not equal to -2. Use a solid line for y \(\small\mathsf{ \geq }\) because 4x + y is less than or equal to 2.
Shade in the Appropriate Areas
Next, shade in the area above the dotted lines because x + y is greater than -2. Now shade in the area below the solid line because 4x + y is less than or equal to 2.
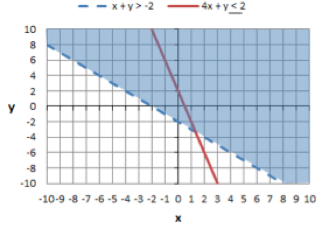
First equation shaded above the dotted line.
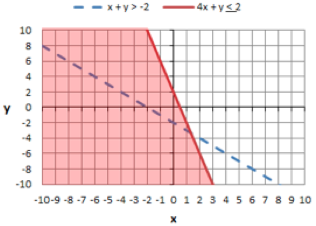
Second equation shaded below the solid line.
The Solution
So, the final solution would be the region where the red and blue shadings overlap:
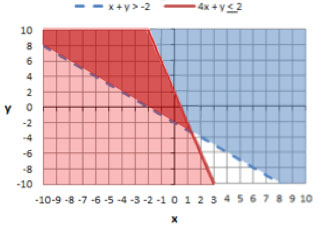
Non-Viable Solutions
Sometimes solutions that you find won't make any sense in the context of the problem. In these cases, you will need to reject the solution. So, when are these cases? Study the example below to find out.
Amy wants to buy at least 20 shirts and tops for her daughters. Shirts were on sale for $12 each and tops were on sale for $3 each. She could spend no more than $120. Use a graph to figure out how many shirts and tops she should buy.
First, let's assign some variables and a system of equations.
Let S = the number of shirts to buy
Let T = the number of tops to buy
The first equation is from "Amy wants to buy at least 20 shirts and tops." The second equation is from "Shirts on sale for $12 each and tops were on sale for $3 each. she could spend no more than $120." This results in:
|
S + T > 20 |
| 12S + 3T \(\small\mathsf{ \leq }\) 120 |
Next, we graph the two lines along with their shaded regions:
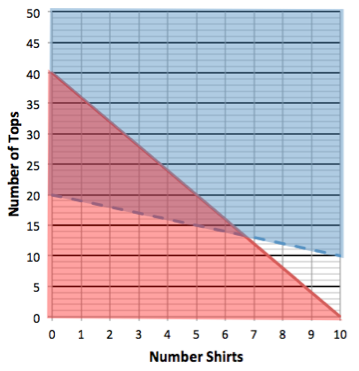
The first equation, S + T > 20 is a dotted line because the inequality does not have an equals sign. It is shaded blue above the line because the inequality is greater than (>).
The second equation, 12S + 3T \(\small\mathsf{ \leq }\) 120 is a solid line because the inequality has an equal sign. It is shaded red below the line because the inequality is less than or equal to (<).
Next, by looking at the graph, the lines intersect at an estimated point of (6.7, 13.30).
Question
Why doesn't this work?
