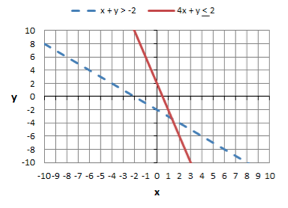
Practice graphing the system of inequalities below. Graph this system and shade in the correct areas.
 |
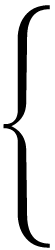x + y > -2 4x + y \(\small\mathsf{ \leq}\) 2 |
 |
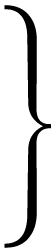Click through the slideshow to check your answer.
|
First draw the lines for the graphs.
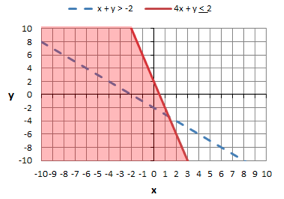
Next, shade in the area above the dotted lines because x + y is greater than -2. Choose a light enough color to see the lines.
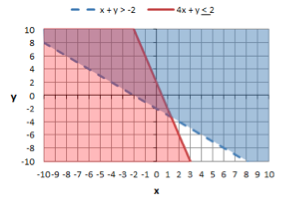
Now shade in the area below the solid line because 4x + y is less than or equal to 2. Here is the graph with just the shading for equation 2.
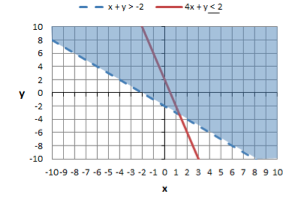
Here is the graph with both equations shaded:
The solution is any coordinate in the area where the shading overlaps. For example, (0,0) is in the overlapping area. Let's check to see if (0,0) is true for both equations. x + y > -2 0 + 0 > -2 (True) Another solution in the shaded area is (-5,6). Let's check this solution:
|
 |
