Looking at the Data

Let's calculate the slope of our landing plane.

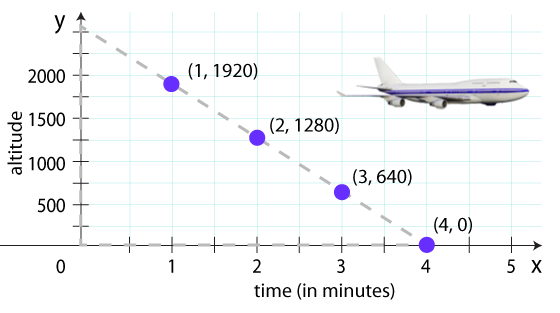
graph of plane descending

Let's look at our landing plane's ordered pairs in a t-chart.

Now let's calculate the rate of change, or slope. Remember that slope is calculated:
m = $\mathsf{ \frac{\text{rise}}{\text{run}} }$

Time Span	Slope
(1, 1920) to (2, 1280)	$\mathsf{ \frac{\text{rise}}{\text{run}} = \frac{1280-1920}{2-1} = \frac{-640\text{ft}}{1\text{min}} }$
(2, 1280) to (3, 640)	$\mathsf{ \frac{\text{rise}}{\text{run}} = \frac{640-1280}{2-3} = \frac{-640\text{ft}}{1\text{min}} }$
(3, 640) to (4, 0)	$\mathsf{ \frac{\text{rise}}{\text{run}} = \frac{0-640}{3-4} = \frac{-640\text{ft}}{1\text{min}} }$

Notice that the slope is always $\mathsf{ \frac{-640\text{ft}}{1\text{min}} }$ .

Let's take a closer look at the slope of our landing airplane.