Before you take a scored quiz for this lesson, try this set of practice questions. How well you score on this self-check will be similar to your scored quiz. If you do not score well on this self-check, please review this lesson and try again.
Which statement is true about the function represented by this graph?
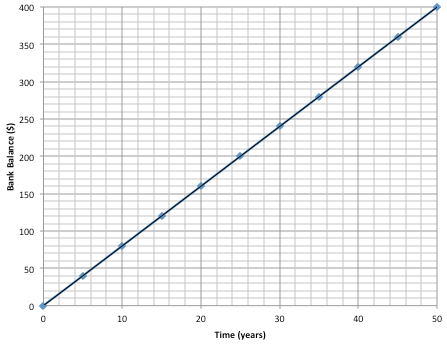
- This graph has a negative slope and shows an object moving up a hill.
- This graph has a positive slope and shows an object moving up a hill.
- This graph has a negative slope and shows increase in dollars over years.
- This graph has a positive slope and shows increase in dollars over years.
The slope is positive since the line is rising to the right. Look at the labels on the x and y axes. This graph is about money in a bank, not about moving uphill.
The slope is positive since the line is rising to the right. Look at the labels on the x and y axes. This graph is about money in a bank, not about moving uphill.
The slope is positive since the line is rising to the right. You are correct that this graph is about money in a bank.
This graph is about money and has a positive slope since the line is rising to the right.
Use the data in the table to calculate the rate of change of the growth of the plant.
| Time (week) | Growth (cm) |
| 2 | 8 |
| 6 | 16 |
| 10 | 24 |
| 12 | 28 |
- 0.5 cm/wk
- 2 cm/wk
- 2.4 cm/wk
- 4 cm/wk
Choose 2 points. Divide the change in the growth by the change in time. Point 1 (6,16) Point 2 (10,24) Slope is \(\mathsf{ \frac{y_2 - y_1}{x_2 - x_1} }\) = \(\mathsf{ \frac{24 - 16}{10 - 6} }\) = \(\mathsf{ \frac{8 cm}{4 weeks} }\) = 2 cm/wk
Choose 2 points. Divide the change in the growth by the change in time. Point 1 (6,16) Point 2 (10,24) Slope is \(\mathsf{ \frac{y_2 - y_1}{x_2 - x_1} }\) = \(\mathsf{ \frac{24 - 16}{10 - 6} }\) = \(\mathsf{ \frac{8 cm}{4 weeks} }\) = 2 cm/wk
Choose 2 points. Divide the change in the growth by the change in time. Point 1 (6,16) Point 2 (10,24) Slope is \(\mathsf{ \frac{y_2 - y_1}{x_2 - x_1} }\) = \(\mathsf{ \frac{24 - 16}{10 - 6} }\) = \(\mathsf{ \frac{8 cm}{4 weeks} }\) = 2 cm/wk
Choose 2 points. Divide the change in the growth by the change in time. Point 1 (6,16) Point 2 (10,24) Slope is \(\mathsf{ \frac{y_2 - y_1}{x_2 - x_1} }\) = \(\mathsf{ \frac{24 - 16}{10 - 6} }\) = \(\mathsf{ \frac{8 cm}{4 weeks} }\) = 2 cm/wk
What is the slope of line AB?
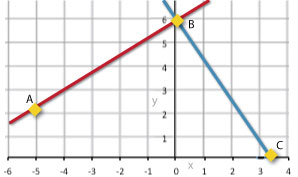
- + \(\mathsf{ \frac{4}{5} }\)
- + \(\mathsf{ \frac{5}{4} }\)
- - \(\mathsf{ \frac{4}{5} }\)
- - \(\mathsf{ \frac{5}{4} }\)
The slope is \(\mathsf{ \frac{rise}{run} }\). Traveling from point A to point B, we move 4 units up (rise) and 5 units right (run). So, the slope is + \(\mathsf{ \frac{4}{5} }\).
The slope is \(\mathsf{ \frac{rise}{run} }\). Traveling from point A to point B, we move 4 units up (rise) and 5 units right (run). So, the slope is + \(\mathsf{ \frac{4}{5} }\).
The slope is \(\mathsf{ \frac{rise}{run} }\). Traveling from point A to point B, we move 4 units up (rise) and 5 units right (run). So, the slope is + \(\mathsf{ \frac{4}{5} }\).
The slope is \(\mathsf{ \frac{rise}{run} }\). Traveling from point A to point B, we move 4 units up (rise) and 5 units right (run). So, the slope is + \(\mathsf{ \frac{4}{5} }\).
What is the slope of line BC?

- + \(\mathsf{ \frac{3}{6} }\)
- - \(\mathsf{ \frac{3}{6} }\)
- + 2
- - 2
The slope is change in y divided by change in x. The ordered pairs are (0,6) and (3,0). Slope = \(\mathsf{ \frac{y_2 - y_1}{x_2 - x_1} }\) = \(\mathsf{ \frac{0 - 6}{3 - 0} }\) = - \(\mathsf{ \frac{6}{3} }\) = -2 Traveling from point B to C, we move 6 units down (rise) and move 3 left (run). So the slope is -\(\mathsf{ \frac{6}{3} }\) or -2.
The slope is change in y divided by change in x. The ordered pairs are (0,6) and (3,0). Slope = \(\mathsf{ \frac{y_2 - y_1}{x_2 - x_1} }\) = \(\mathsf{ \frac{0 - 6}{3 - 0} }\) = - \(\mathsf{ \frac{6}{3} }\) = -2 Traveling from point B to C, we move 6 units down (rise) and move 3 left (run). So the slope is -\(\mathsf{ \frac{6}{3} }\) or -2.
The slope is change in y divided by change in x. The ordered pairs are (0,6) and (3,0). Slope = \(\mathsf{ \frac{y_2 - y_1}{x_2 - x_1} }\) = \(\mathsf{ \frac{0 - 6}{3 - 0} }\) = - \(\mathsf{ \frac{6}{3} }\) = -2 Traveling from point B to C, we move 6 units down (rise) and move 3 left (run). So the slope is -\(\mathsf{ \frac{6}{3} }\) or -2.
The slope is change in y divided by change in x. The ordered pairs are (0,6) and (3,0). Slope = \(\mathsf{ \frac{y_2 - y_1}{x_2 - x_1} }\) = \(\mathsf{ \frac{0 - 6}{3 - 0} }\) = - \(\mathsf{ \frac{6}{3} }\) = -2 Traveling from point B to C, we move 6 units down (rise) and move 3 left (run). So the slope is -\(\mathsf{ \frac{6}{3} }\) or -2.
Calculate the rate of change of the motion of the pelican shown in this graph.
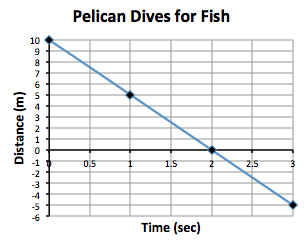
- +10 m/s
- -10 m/s
- +5 m/s
- -5 m/s
- +\(\mathsf{ \frac{1m}{5s} }\)
- -\(\mathsf{ \frac{1m}{5s} }\)
The slope is change in y divided by change in x. Choose two ordered pairs are (1,5) and (3,-5). Slope = \(\mathsf{ \frac{y_2 - y_1}{x_2 - x_1} }\) = \(\mathsf{ \frac{-5 - 5}{3 - 1} }\) = \(\mathsf{ \frac{-10}{2} }\) = -5
The slope is change in y divided by change in x. Choose two ordered pairs are (1,5) and (3,-5). Slope = \(\mathsf{ \frac{y_2 - y_1}{x_2 - x_1} }\) = \(\mathsf{ \frac{-5 - 5}{3 - 1} }\) = \(\mathsf{ \frac{-10}{2} }\) = -5
The slope is change in y divided by change in x. Choose two ordered pairs are (1,5) and (3,-5). Slope = \(\mathsf{ \frac{y_2 - y_1}{x_2 - x_1} }\) = \(\mathsf{ \frac{-5 - 5}{3 - 1} }\) = \(\mathsf{ \frac{-10}{2} }\) = -5
The slope is change in y divided by change in x. Choose two ordered pairs are (1,5) and (3,-5). Slope = \(\mathsf{ \frac{y_2 - y_1}{x_2 - x_1} }\) = \(\mathsf{ \frac{-5 - 5}{3 - 1} }\) = \(\mathsf{ \frac{-10}{2} }\) = -5
The slope is change in y divided by change in x. Choose two ordered pairs are (1,5) and (3,-5). Slope = \(\mathsf{ \frac{y_2 - y_1}{x_2 - x_1} }\) = \(\mathsf{ \frac{-5 - 5}{3 - 1} }\) = \(\mathsf{ \frac{-10}{2} }\) = -5
The slope is change in y divided by change in x. Choose two ordered pairs are (1,5) and (3,-5). Slope = \(\mathsf{ \frac{y_2 - y_1}{x_2 - x_1} }\) = \(\mathsf{ \frac{-5 - 5}{3 - 1} }\) = \(\mathsf{ \frac{-10}{2} }\) = -5
Summary
 Questions answered correctly:
Questions answered correctly:
 Questions answered incorrectly:
Questions answered incorrectly:
Rate of Change
Graphs can be used to model how changing one variable in a relationship affects the other.Specifically, we can model how changing the x variable will change the y variable.
A rate is the ratio of two variables. We measure rate of change as \(\mathsf{ \frac{y_2-y_1}{x_2-x_1} }\).
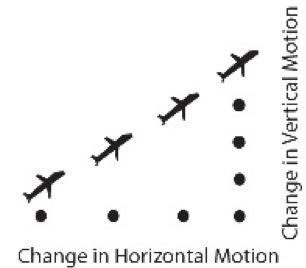
Question
A plane takes off from the runway. For each meter the plane moves forward, the plane rises by 8 meters. The rate of change in altitude is:
positive 8
Rate of Change
Question
A plant grows 5 cm each week. The rate of change in plant growth is:
positive 5
Question
Jeremy earns $5 for each 8 boxes assembled. The rate of change in Jeremy’s income is:
positive \(\mathsf{ \frac{5}{8} }\)
Finding Slope Using a Data Table
Rate of change can be expressed mathematically as the slope of the line. Slope is change in y divided by change in x. Remember that x is the domain and y is the range. The equation for slope = \(\mathsf{ \frac{y_2-y_1}{x_2-x_1} }\).
| time (week) | plant growth (cm) |
| 2 | 8 |
| 6 | 16 |
| 10 | 24 |
| 12 | 28 |
Choose any two points to find the slope. In this case, let's choose the points (2,8) and (6,16). (2,8)=(\(\mathsf{ x_1 }\),\(\mathsf{ y_1 }\)) (6,16) = (\(\mathsf{ x_2 }\),\(\mathsf{ y_2 }\))
Use the slope formula to find the rate of change in plant growth.
slope=\(\mathsf{ \frac{y_2-y_1}{x_2-x_1} }\)=\(\mathsf{ \frac{16-8}{6-2} }\)=\(\mathsf{ \frac{8}{4} }\)=2 or 2 cm per week
Finding Slope Using a Data Table
Try this problem on your own. Click the answer button to reveal the solution:
| # Sweaters Made | Ami’s Salary (Dirhams) |
| 2 | 240 |
| 5 | 600 |
| 7 | 840 |
According to the table, what is the rate of change for Ami’s work?
(Note: The currency in Morocco is the dirham.)
Finding Slope Using Domain and Range
Suppose the domain is (3, 7, 11, 15) and the range is (5, 7, 9, 11).
First, write the points from what you are given.:(3, 5), (7,7), (11,9) and (15, 11)
Next, choose any two ordered pairs. For this example, lets use (7,7) and (11,9)
slope=\(\mathsf{ \frac{y_2-y_1}{x_2-x_1} }\)=\(\mathsf{ \frac{9-7}{11-7} }\)=\(\mathsf{ \frac{2}{4} }\)=\(\mathsf{ \frac{1}{2} }\)
The slope is:\(\mathsf{ \frac{1}{2} }\) or positive one-half.
Finding Slope Using Two Ordered Pairs
For the weight loss of a sumo wrestler, calculate the rate of change in kilograms per day. (0, 150) (5, 130)
Identify the first and second points. (0, 150)=(\(\mathsf{ x_1 }\),\(\mathsf{ y_1 }\)) (5, 130)=(\(\mathsf{ x_2 }\),\(\mathsf{ y_2 }\))
slope=\(\mathsf{ \frac{y_2-y_1}{x_2-x_1} }\)=\(\mathsf{ \frac{150-130}{0-5} }\)=\(\mathsf{ \frac{20}{-5} }\)=-4
The weight lost is 4 kilograms per day. Notice how the rate of change (slope) is negative. This is because we are dealing with weight loss.
Finding Slope Using Two Data Points
Try this problem on your own. Click the answer button to check your final answer:
Question
Ben’s bank balance changed from $50 in January to $250 in April. What was the rate of change?
January is month 1, and april is month 4
Rate of change=slope=\(\mathsf{ \frac{y_2-y_1}{x_2-x_1} }\)=\(\mathsf{ \frac{250-50}{4-1} }\)=\(\mathsf{ \frac{200}{3} }\)=$66.67 a month.
Finding Slope Using a Graph
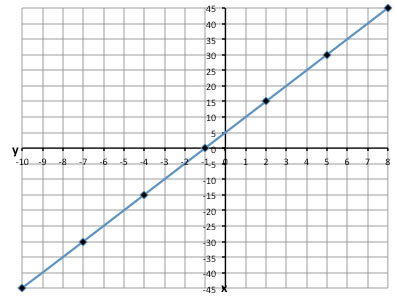
Choose 2 convenient points and write them as ordered pair. Let’s choose (-10,-45)=(\(\mathsf{ x_1 }\),\(\mathsf{ y_1 }\)) (8,45)=(\(\mathsf{ x_2 }\),\(\mathsf{ y_2 }\))
Slope=\(\mathsf{ \frac{y_2-y_1}{x_2-x_1} }\)=\(\mathsf{ \frac{45--45}{8--10} }\)=\(\mathsf{ \frac{90}{18} }\)= positive 5.
Finding Slope Using a Graph
Try this problem on your own. Click the answer button to reveal the solution:
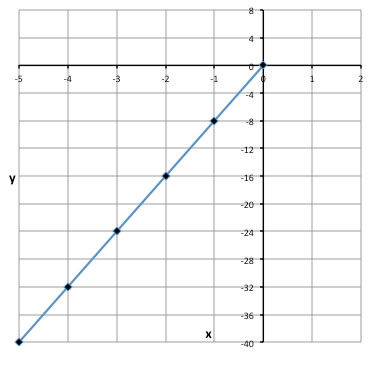
What is the slope of this graph?
The slope is positive. The rise is 8 and the run is 1.
———
Now that you have had some more practice, you should be better prepared for your quiz. If you still do not feel confident about any topics, please contact your teacher for some additional help.

