You can use the coordinate plane to graph both horizontal and vertical lines. In a previous lesson, you learned that you can use the coordinate plane to graph lines that have a positive slope and those that have a negative slope. In each of these instances, you were told the coordinates of the ordered pairs you needed to graph to create a certain line. Once you graphed that line, then you were able to calculate its slope.
But you can also use the graph of a line to determine its slope by using the slope formula.
The Slope Formula
The slope formula is \( m = \frac{\text{rise}}{\text{run}} = \frac{y_{2} - y_{1}}{x_{2} - x_{1}} \).
In this formula, \( (x_{1},\ y_{1}) \) represent the coordinates of one known point on the line, and \( (x_{2},\ y_{2}) \) represent the coordinates of the other known point on the line.
In the video below, the instructor will show you how to read a graph to determine if a line has a positive, negative, 0, or undefined slope. Then, he will show you how to choose points along the graph of the line to confirm your slope reading is correct. Pay close attention to how the instructor determines which points to use in the slope formula.
To determine the slope of a line from its graph, the process is virtually identical to when we calculate slope using ordered pairs, but we just have to find those ordered pairs ourselves. The steps for finding the slope from a graph are, first, examine the graph of the line to determine if the slope if positive, negative, 0, or undefined. Next, choose two ordered pairs that lie along the line. You can choose any two ordered pairs, so long as both of them are on the line. Lastly, substitute the ordered pairs into the slope formula and then simplify to show that your slope categorization is correct.
As an example of this process, let's look at this graph here. We can tell, because the graph slopes down as we move right, that this line has a negative slope. Now, let's verify this. We'll pick two points that lie on this line. There are so many options, but I'll pick this point here, negative 5, 5, and this point here, negative 2, negative 1. Now we can substitute these values into the slope formula, which is m equals y2 minus y1 over x2 minus x1. First, let's substitute in our x- and y-values from point 1, then our x- and y-values from point 2. And now we simplify. Negative 1 minus 5 is negative 6, and negative 2 minus negative 5 is 3. Negative 6 over 3 simplifies to negative 2. We were right, this line does have a negative slope.
Recall that if the line had gotten higher as we moved to the right, like this, it would have had a positive slope. If it had been horizontal, like this, it would have had zero slope, and if it had been vertical, like this, it's slope would be undefined.
Let's go over to the whiteboard to work on a few more examples together.
This question asks, "Is the slope of the line as shown in the graph, positive, negative, zero, or undefined? Calculate the slope value to show your answer is correct." Well, looking at this line, as we move from left to right, it's rising. So that tells us that this line has a positive slope. Now we can choose two points on the line and calculate the slope to see if this is correct. So I see one point here, and that's negative 4, 0, and then one point here, which is 0, 1. So let's write those points down. That's negative 4, 0, and 0, 1. Recall that the slope formula is m equals y2 minus y1 over x2 minus x1. So let's substitute in the values that we're given. Y2 is the y-value from our second point, so that's 1, minus the y value from our first point, which is 0, over x2 minus x1. Well the x-value from our second point is 0, minus the x-value from our first point is negative 4. 1 minus 0 is 1, and 0 minus negative 4 is the same as 0 plus positive 4, which is 4. And this is as much as we can simplify this, so the slope, m, of this line is 1 over 4, one fourth. And this is a positive value, which is exactly what we expected. So our expectation was correct. Alright, let's look at another one.
Here we're asked the same question, but the line we're given is a vertical line. And recall that vertical lines have an undefined slope. So let's write that down. But we can still use the slope formula to show that this is correct, and that's m equals y2 minus y1 over x2 minus x1. So let's pick two points on this line, maybe this one here, which is negative 6, 0, and we'll pick this one here, which is negative 6, 3. So that's negative 6, 0 and negative 6, 3. Let's substitute these values into our slope equation. Y2, which is the y-value on our second point, is 3. Minus y1, which is the y-value on our first point, or 0, over x2, which is the x-value on our second point, or negative 6, minus x1, which is the x-value on our first point, which is also negative 6. 3 minus 0 is 3, and negative 6 minus negative 6 is the same as negative 6 plus positive 6, which is 0, and 3 divided by 0 is undefined, because we cannot divide any number by 0. So we were correct in asserting that this has an undefined slope. Alright, let's look at one last example.
Again, we're asked the same question, but this time our line is horizontal. Horizontal lines have zero slope, but let's prove this using the slope formula of m equals y2 minus y1 over x2 minus x1. So let's pick two points on this line. We'll pick this point right here of 0, negative 5, and this point right here, which is 3, negative 5. Now let's substitute these values into the slope equation. Y2 is the y-value on our second point, which is negative 5, minus y1, the y-value on our first point, which is also negative 5. That is over x2, the x-value on our second point, which is 3, minus x1, the x-value on our first point, which is 0. Negative 5 minus negative 5 is the same as negative 5 plus positive 5, which is 0, and 3 minus 0 is 3. And 0 divided by 3 is 0. So we were correct that this line has zero slope.
Question
Nicholas is trying to calculate the slope of the line shown on the graph below. He chooses the ordered pairs (1, 2) and (2, 1) to substitute into the slope formula to show the slope of this line is 0. Can you use these ordered pairs to calculate the slope of this line?
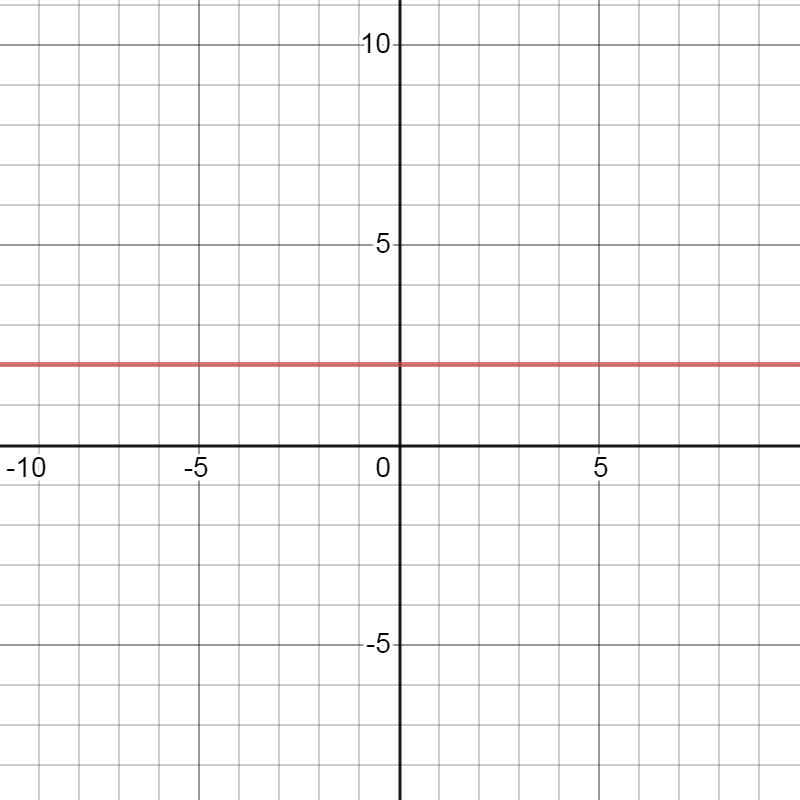
A line on the coordinate plane. The line is perfectly flat as you read it from left to right. Points on the line include:
- (-8,2)
- (-4,2)
- (1,2)
- (2,2)
No, because the ordered pair (2, 1) does not lie on this line.
