You can use the graph of a line to determine its slope by following the steps shown below.
- Examine the graph of the line to determine if the slope if positive, negative, 0, or undefined.
- Choose two ordered pairs that lie along the line.
You can choose any two ordered pairs, so long as both of them are on the line. - Substitute the ordered pairs into the slope formula and then simplify to show that your slope categorization is correct.
Remember
- Lines that increase as you read them from left to right have a positive slope.
- Lines that decrease as you read them from left to right have a negative slope.
- Lines that are flat are horizontal and have a slope value of 0.
- Lines that run up and down on the coordinate plane are vertical; slope is undefined.
Practice finding the slope of a line from a graph by completing the activity below. Look at the graph on each tab. Decide if the slope is positive, negative, 0, or undefined, and then show you are correct using the slope formula. Be sure to check your answers.
Is the slope of the line shown in the graph positive, negative, 0, or undefined? Calculate the slope value to show your answer is correct.
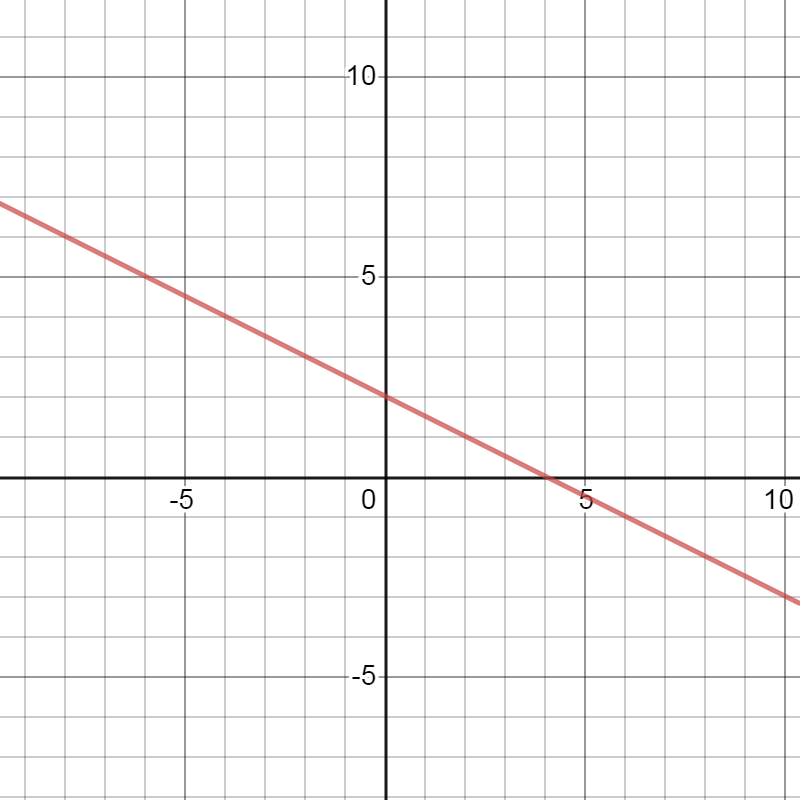
A line on the coordinate plane. The line decreases as you read it from left to right. Points on the line include (0, 2) and (4, 0).
Slope is negative.
\( m = - \frac{1}{2} \)
If you need help arriving at this answer, click the Solution button.
Step 1: Examine the graph of the line to determine if the slope if positive, negative, 0, or undefined. |
The line on the graph decreases as you read it from left to right. The slope is negative. |
Step 2: Choose two ordered pairs that lie along the line. |
You can choose any two ordered pairs, so long as both of them are on the line. Choose (0, 2) and (4, 0). |
Step 3: Substitute the ordered pairs into the slope formula and then simplify to show that your slope categorization is correct. |
\( m = \frac{y_{2} - y_{1}}{x_{2} - x_{1}} \) \( m = \frac{\left( 0 \right) - \left( 2 \right)}{\left( 4 \right) - \left( 0 \right)} \) \( m = \frac{0 - 2}{4 - 0} \) \( m = - \frac{2}{4} \) \( m = - \frac{1}{2} \) |
Is the slope of line C positive, negative, 0, or undefined? Calculate the slope value to show your answer is correct.
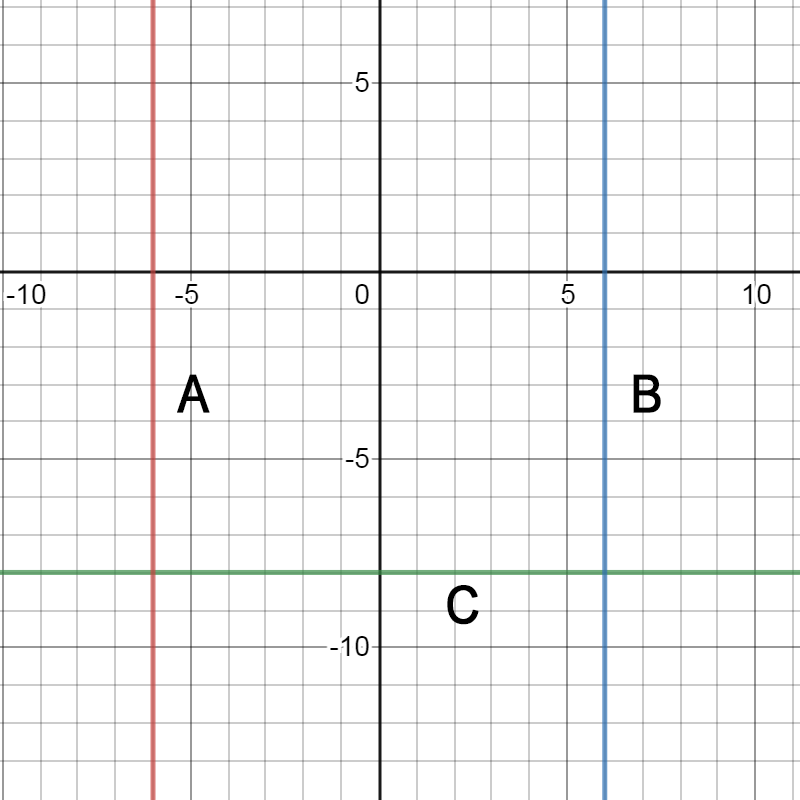
Three lines on the coordinate plane. One is a red line labelled A that runs up and down. The second is a blue line labelled B that runs up and down. The third is a green line labelled C that is perfectly flat as you read it from left to right.
Slope is 0.
\( m = 0 \)
If you need help arriving at this answer, click the Solution button.
Step 1: Examine the graph of the line to determine if the slope if positive, negative, 0, or undefined. |
The line on the graph is flat. This is a horizontal line. The slope is 0. |
Step 2: Choose two ordered pairs that lie along the line. |
Choose any two ordered pairs, so long as both of them are on the line. Choose (0, \( - \)8) and (5, \( - \)8). |
Step 3: Substitute the ordered pairs into the slope formula and then simplify to show that your slope categorization is correct. |
\( m = \frac{y_{2} - y_{1}}{x_{2} - x_{1}} \) \( m = \frac{\left( - 8 \right) - \left( - 8 \right)}{\left( 5 \right) - \left( 0 \right)} \) \( m = \frac{- 8 + 8}{5 - 0} \) \( m = \frac{0}{5} \) \( m = 0 \) |
Is the slope of the line shown in the graph positive, negative, 0, or undefined? Calculate the slope value to show your answer is correct.
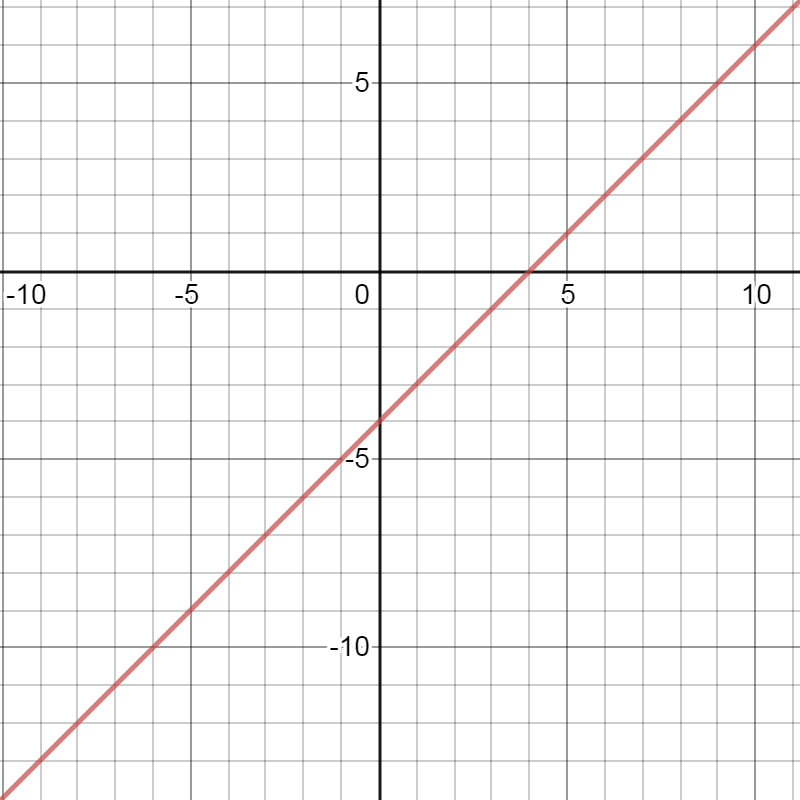
A line on the coordinate plane. The line increases as you read it from left to right. Points on the line include (0, -4) and (4, 0).
Slope is positive.
\( m = 1 \)
If you need help arriving at this answer, click the Solution button.
Step 1: Examine the graph of the line to determine if the slope if positive, negative, 0, or undefined. |
The line on the graph increases as you read it from left to right. Slope is positive. |
Step 2: Choose two ordered pairs that lie along the line. |
Choose any two ordered pairs on the line. Choose (0, \( - \)4) and (4, 0). |
Step 3: Substitute the ordered pairs into the slope formula and then simplify to show that your slope categorization is correct. |
\( m = \frac{y_{2} - y_{1}}{x_{2} - x_{1}} \) \( m = \frac{\left( 0 \right) - \left( - 4 \right)}{\left( 4 \right) - \left( 0 \right)} \) \( m = \frac{0 + 4}{4 - 0} \) \( m = \frac{4}{4} \) \( m = 1 \) |
Is the slope of line B in the graph positive, negative, 0, or undefined? Calculate the slope value to show your answer is correct.

Three lines on the coordinate plane. One is a red line labelled A that runs up and down. The second is a blue line labelled B that runs up and down. The third is a green line labelled C that is perfectly flat as you read it from left to right.
Slope is undefined.
If you need help arriving at this answer, click the Solution button.
Step 1: Examine the graph of the line to determine if the slope if positive, negative, 0, or undefined. |
This is a vertical line. Slope is undefined. |
Step 2: Choose two ordered pairs that lie along the line. |
Choose any two ordered pairs on the line. Choose (6, 1) and (6, 0). |
Step 3: Substitute the ordered pairs into the slope formula and then simplify to show that your slope categorization is correct. |
\( m = \frac{y_{2} - y_{1}}{x_{2} - x_{1}} \) \( m = \frac{\left( - 1 \right) - \left( 0 \right)}{\left( 6 \right) - \left( 6 \right)} \) \( m = \frac{- 1}{\color{#A80000}{0}} \) You cannot divide by 0; the slope is undefined. |
Is the slope of the line shown in the graph positive, negative, 0, or undefined? Calculate the slope value to show your answer is correct.
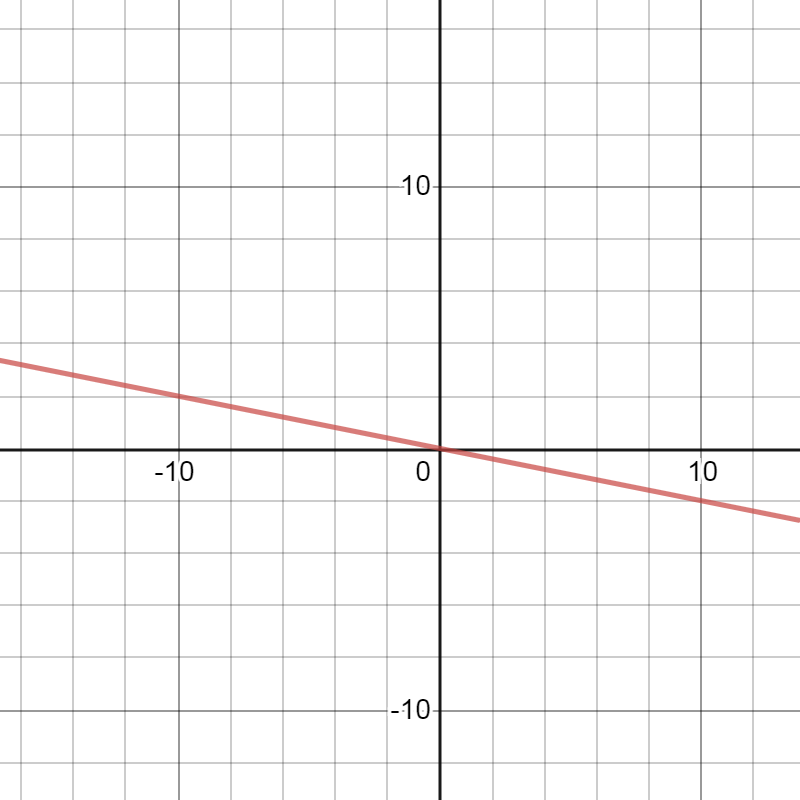
A line on the coordinate plane. The line decreases as you read it from left to right. Points on the line include (0, 0) and (10, -2).
Slope is negative.
\( m = - \frac{1}{5} \)
If you need help arriving at this answer, click the Solution button.
Step 1: Examine the graph of the line to determine if the slope if positive, negative, 0, or undefined. |
The line decreases as you read it from left to right. Slope is negative. |
Step 2: Choose two ordered pairs that lie along the line. |
Choose any two ordered pairs. Choose (0, 0) and (10, \( - \)2). |
Step 3: Substitute the ordered pairs into the slope formula and then simplify to show that your slope categorization is correct. |
\( m = \frac{y_{2} - y_{1}}{x_{2} - x_{1}} \) \( m = \frac{\left( - 2 \right) - \left( 0 \right)}{\left( 10 \right) - \left( 0 \right)} \) \( m = \frac{- 2}{10} \) \( m = - \frac{1}{5} \) |
