Lines in the coordinate plane can have a positive slope or a negative slope. There are also lines in the plane that have a slope value of 0. When a line has a slope value of 0, then that line is horizontal. A horizontal line does not increase or decrease as you read it from left to right. Additionally, all of the ordered pairs that lie along a horizontal line have identical \( y \)-coordinates.
Look at the line shown below.
This line is different than those you have learned about so far. It is a vertical line. A vertical line runs up and down in the coordinate plane. All of the ordered pairs that lie along a vertical line have identical \( x \)-coordinates.
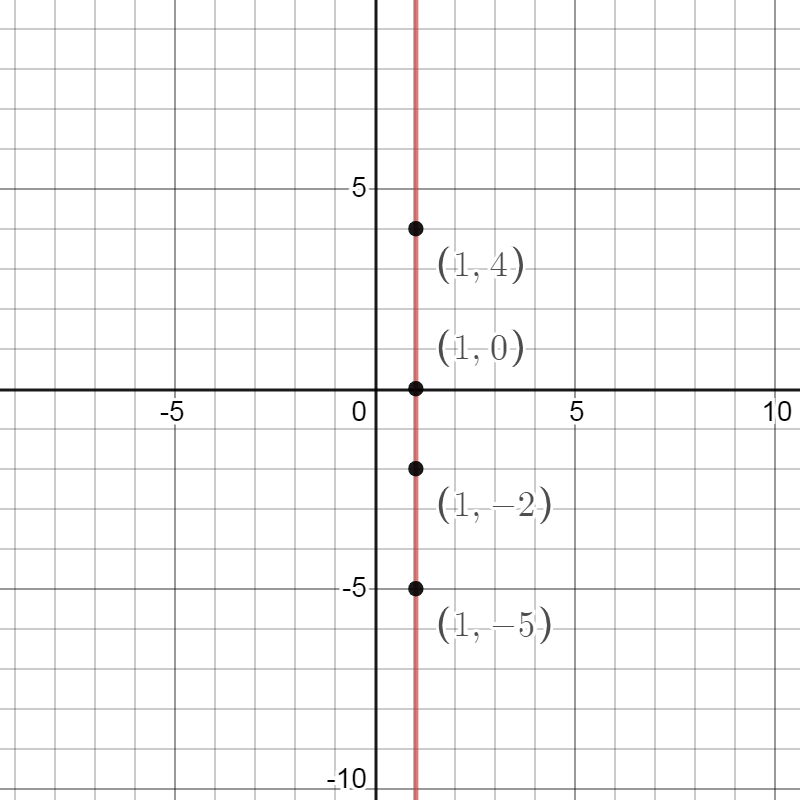
A line on the coordinate plane. The line is runs up and down. The following points on the line are labelled with their ordered pairs:
- (1,4)
- (1,0)
- (1,-2)
- (1,-5)
But what is the slope value of a vertical line? Look at the example below.
What is the slope of the vertical line that passes through the ordered pairs \( (1,\ 4) \) and \( (1, - 2) \)? Use the slope formula, \( m = \frac{\text{rise}}{\text{run}} = \frac{y_{2} - y_{1}}{x_{2} - x_{1}} \), to calculate.
Step 1: Label the given ordered pairs as \( (x_{1},\ y_{1}) \) and \( (x_{2},\ y_{2}) \). |
Let \( \left( x_{1},\ y_{1} \right) = (1,\ 4) \) Let \( \left( x_{2},\ y_{2} \right) = (1, - 2) \) Remember that it does not matter which ordered pair is assigned to be \( (x_{1},\ y_{1}) \) or \( (x_{2},\ y_{2}) \). |
Step 2: Substitute the values into the slope formula and simplify. |
\( m = \frac{y_{2} - y_{1}}{x_{2} - x_{1}} \) \( m = \frac{\left( - 2 \right) - (4)}{\left( 1 \right) - (1)} \) \( m = \frac{- 2 - 4}{1 - 1} \) \( m = \frac{- 6}{\color{#A80000}{0}} \) |
The value of the denominator simplifies to 0. Division by 0 is always undefined, so the slope of a vertical line is undefined. |
|
The slope of a vertical line is undefined. This is different than the slope of a horizontal line, which is 0. A horizontal line has a slope of 0 because it has no steepness. In contrast, a vertical line is infinitely steep! Because the denominator of the slope equation is 0 and division by 0 is undefined, the slope of a vertical line is undefined.
How well do you understand vertical lines in the coordinate plane? Use the activity below to find out. Answer each question, and then compare your answers to the sample answers.
1. Why is the slope of a vertical line undefined?
2. What is true about the \( x \)-coordinates of all the ordered pairs that lie along a vertical line?
| Your Responses | Sample Answers |
|---|---|
The slope of a vertical line is undefined because the denominator of the slope equation is 0 for every vertical line. Division by 0 is undefined. |
|
The \( x \)-coordinates of all the ordered pairs that lie along a vertical line are identical. |
|
