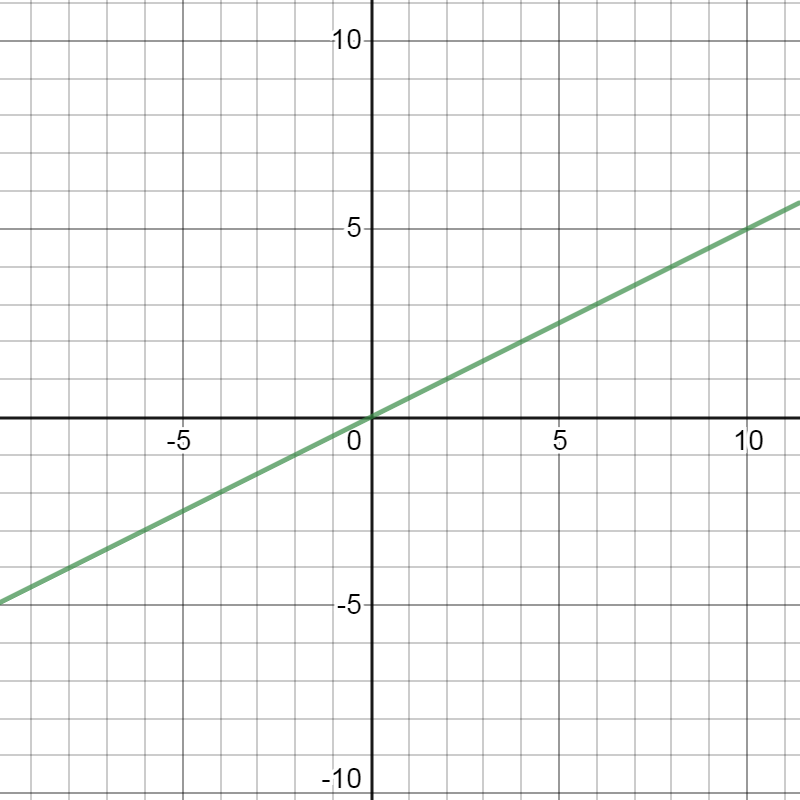
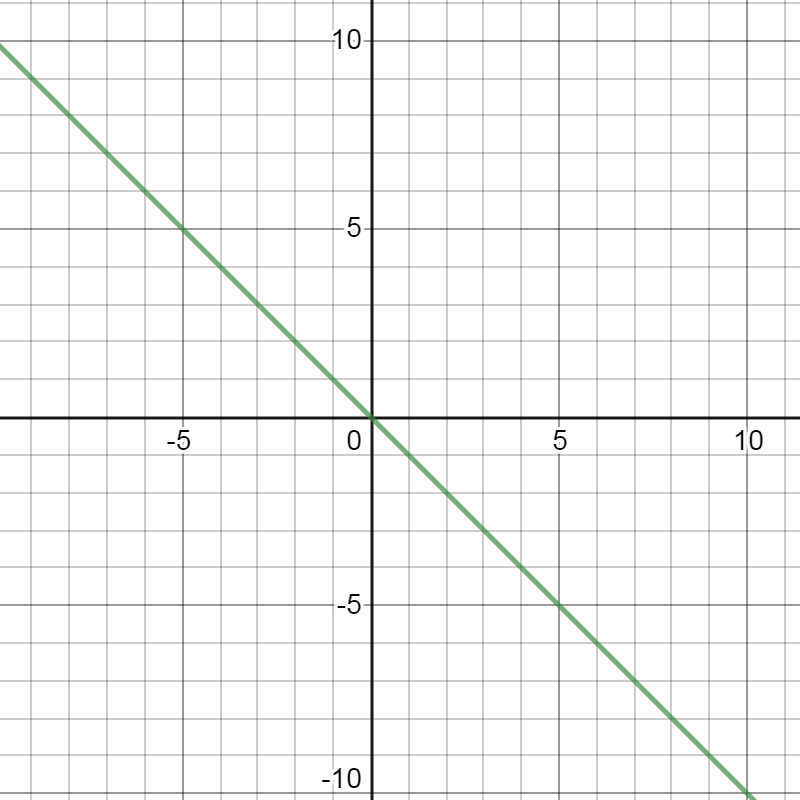
The slope of a line measures its steepness. Sometimes a slope value is positive, such as \( m = \frac{1}{2} \). In other cases, the slope value is negative, like \( m = - \frac{1}{2} \). It is also possible for the value of a slope to be equal to 0.
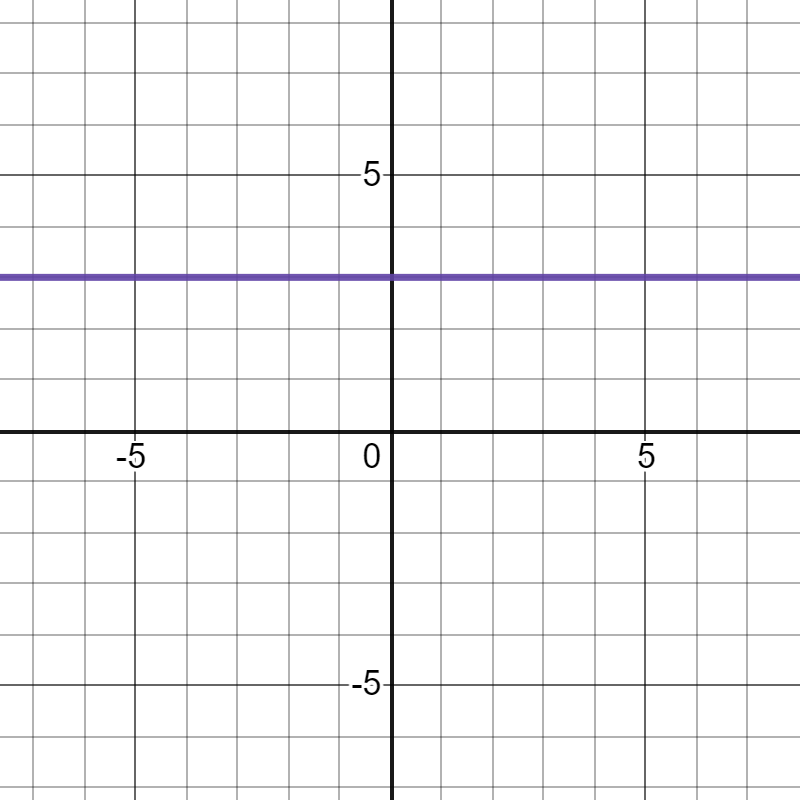
Look at the graphs below. What is different about the line pictured in the graph farthest to the right? Click each graph to take a closer look and to read about its slope.
When a line has a slope value of 0, then that line is horizontal. A slope value of 0 means that the line does not rise or fall as you read it from left to right. All of the ordered pairs that lie along a horizontal line have identical \( y \)-coordinates.
Look at the image shown. This line has a slope of 0. You know that because it does not rise or fall as you read it from left to right in the coordinate plane, and the \( y \)-coordinate of every ordered pair that lies along this line is 3. This line is horizontal.
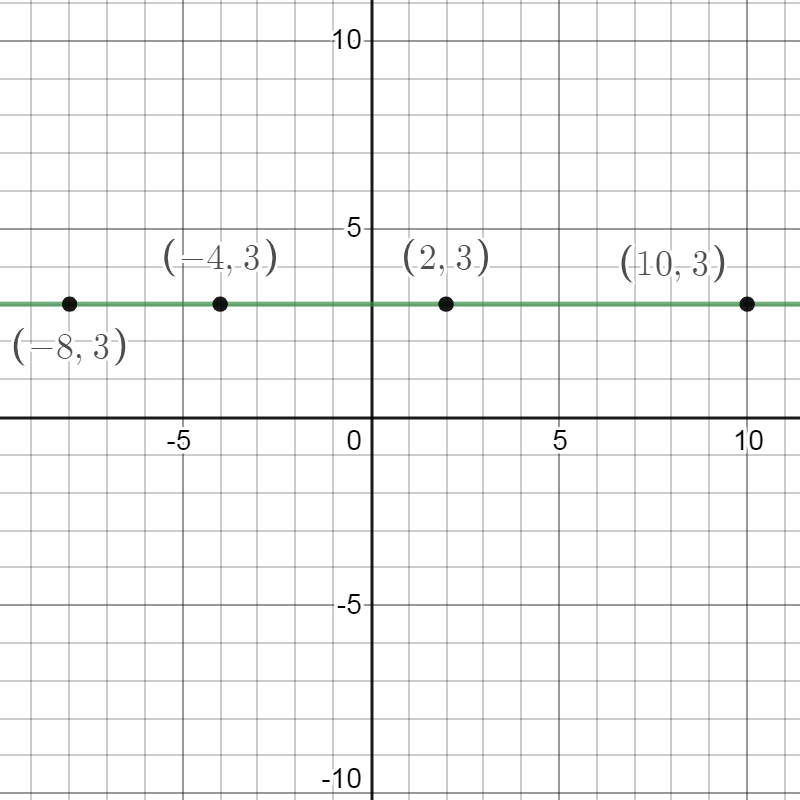
A line on the coordinate plane. The line is perfectly flat as you read it from left to right. The following points on the line are labelled with their ordered pairs:
- (-8,3)
- (-4,3)
- (2,3)
- (10,3)
It is important to be able to determine if a line is horizontal both by reading the graph and by examining the ordered pairs that lie along the line. In the activity below, you will see sets of ordered pairs. Click on the set of ordered pairs that lie along a horizontal line.
Remember that the \( y \)-coordinates of every ordered pair on a horizontal line are identical.
1. Which ordered pairs lie along a horizontal line?
Look for the ordered pairs that have identical \( y \)-coordinates. The ordered pairs \( (6, - 5) \) and \( ( - 9, - 5) \) lie along a horizontal line because they have identical \( y \)-coordinates.
The ordered pairs \( (6, - 5) \) and \( ( - 9, - 5) \) lie along a horizontal line because they have identical \( y \)-coordinates.
Look for the ordered pairs that have identical \( y \)-coordinates. The ordered pairs \( (6, - 5) \) and \( ( - 9, - 5) \) lie along a horizontal line because they have identical \( y \)-coordinates.
2. Which ordered pairs lie along a horizontal line?
The ordered pairs \( \left( - \frac{1}{2},\frac{3}{4} \right) \) and \( \left( \frac{1}{2},\frac{3}{4} \right) \) lie along a horizontal line because they have identical \( y \)-coordinates.
Look for the ordered pairs that have identical \( y \)-coordinates. The ordered pairs \( \left( - \frac{1}{2},\frac{3}{4} \right) \) and \( \left( \frac{1}{2},\frac{3}{4} \right) \) lie along a horizontal line because they have identical \( y \)-coordinates.
Look for the ordered pairs that have identical \( y \)-coordinates. The ordered pairs \( \left( - \frac{1}{2},\frac{3}{4} \right) \) and \( \left( \frac{1}{2},\frac{3}{4} \right) \) lie along a horizontal line because they have identical \( y \)-coordinates.
3. Which ordered pairs lie along a horizontal line?
Look for the ordered pairs that have identical \( y \)-coordinates. The ordered pairs \( (0,\ 0) \) and \( ( - 3,\ 0) \) lie along a horizontal line because they have identical \( y \)-coordinates.
Look for the ordered pairs that have identical \( y \)-coordinates. The ordered pairs \( (0,\ 0) \) and \( ( - 3,\ 0) \) lie along a horizontal line because they have identical \( y \)-coordinates.
The ordered pairs \( (0,\ 0) \) and \( ( - 3,\ 0) \) lie along a horizontal line because they have identical \( y \)-coordinates.
You got # out of # correct. Click the Retry button for another attempt.
You got a perfect score. Great job!