Previously, you learned that you can use the properties of inequality, along with inverse operations, to help you solve inequalities by isolating the variable. The properties of inequality are reviewed below.
For all the real numbers \( a,\ b, \) and \( c \):
The Addition Property of Inequality |
If \( a > b, \) then \( a + c > b + c \) |
|---|---|
The Subtraction Property of Inequality |
If \( a > b \), then \( a - c > b - c \) |
The Multiplication Property of Inequality |
If \( a > b \) and \( c > 0 \), then \( ac > bc \) If \( a > b \) and \( c < 0 \), then \( ac < bc \) |
The Division Property of Inequality |
If \( a > b \) and \( c > 0 \), then \( \frac{a}{c} > \frac{b}{c} \) If \( a > b \) and \( c < 0 \), then \( \frac{a}{c} < \frac{b}{c} \) |
Sometimes, you need to use the distributive property when solving inequalities. Remember, this property allows you to multiply a sum or difference by multiplying each part of the sum or difference individually. Once an inequality is solved, you can graph its solution using a number line. All the numbers that are included in the shaded area are solutions of the inequality. For example:
Solve \( \frac{x}{4} - 7 \gt - 3 \).
Graph your solution on a number line.
The steps for solving inequalities using the properties of inequality and inverse operations are shown in the table below. Click each step to see it applied to the example.
You do not need to use the distributive property for this inequality. |
|
Start by applying the addition property of inequality. \( \frac{x}{4} - 7 \gt - 3 \) \( \frac{x}{4} - 7 \color{#A80000}{+ 7} \gt - 3 \color{#A80000}{+ 7} \) \( \frac{x}{4} \gt 4 \) Now use the multiplication property of inequality. \( \color{#A80000}{\bcancel{4} \cdot} \frac{x}{\bcancel{4}} \gt 4 \color{#A80000}{\cdot 4} \) \( x \gt 16 \) |
|

The inequality \( x \gt 16 \) on a number line. |
|
Choose any value that is in the shaded area. Substitute \( x = 20 \). \( \frac{(20)}{4} - 7 \gt - 3 \) \( 5 - 7 \gt - 3 \) \( - 2 \gt - 3 \) |
Use the activity below to see how well you remember how to use the distributive property and the properties of equality to solve inequalities. Answer the question on each tab, then check your answer.
Solve \( 3 \leq - x - \frac{1}{4} \).
Graph your solution on a number line.
\( - 3\frac{1}{4} \geq x \)

The inequality \( - 3\frac{1}{4} \geq x \) on a number line.
If you need help arriving at this answer, click the Solution button.
Step 1: Apply the distributive property as needed. |
You do not need to use the distributive property for this inequality. |
Step 2: Solve using inverse operations and the properties of inequality. |
Use the addition property of equality. \( 3 \leq - x - \frac{1}{4} \) \( 3 \color{#A80000}{+ \frac{1}{4}} \leq - x - \frac{1}{4} \color{#A80000}{+ \frac{1}{4}} \) \( 3\frac{1}{4} \leq - x \) Use the division property of equality. Since you divide by a negative number, the inequality reverses direction. \( \frac{3\frac{1}{4}}{\color{#A80000}{- 1}} \leq - \frac{x}{\color{#A80000}{- 1}} \) \( - 3\frac{1}{4} \geq x \) |
Step 3: Graph the solution on a number line. |

The inequality \( - 3\frac{1}{4} \geq x \) on a number line. |
Step 4: Check your shading. |
Choose any value that is in the shaded area. Substitute \( x = - 5 \) \( 3 \leq - ( - 5) - \frac{1}{4} \) \( 3 \leq 5 - \frac{1}{4} \) \( 3 \leq 4\frac{3}{4} \) |
Solve \( 22 \leq 4(2x - 6) \).
Graph your solution on a number line.
\( 5.75 \leq x \)

The inequality \( 5.75 \leq x \) on a number line.
If you need help arriving at this answer, click the Solution button.
Step 1: Apply the distributive property as needed. |
Apply the distributive property to the right-hand side. \( 22 \leq 4\left( 2x - 6 \right) \) \( 22 \leq 8x - 24 \) |
Step 2: Solve using inverse operations and the properties of inequality. |
Start with the addition property of inequality and then use the division property of inequality. \( 22 \leq 8x - 24 \) \( 22 \color{#A80000}{+ 24} \leq 8x - 24 \color{#A80000}{+ 24} \) \( \frac{46}{\color{#A80000}{8}} \leq \frac{\bcancel{8}x}{\color{#A80000}{\bcancel{8}}} \) \( 5.75 \leq x \) |
Step 3: Graph the solution on a number line. |

The inequality \( 5.75 \leq x \) on a number line. |
Step 4: Check your shading. |
Choose any value that is in the shaded area. Substitute \( x = 6 \) \( 22 \leq 4\left( 2(6) - 6 \right) \) \( 22 \leq 4\left( 12 - 6 \right) \) \( 22 \leq 4\left( 6 \right) \) \( 22 \leq 24 \) |
Solve \( - 1.5\left( 2x + 4.5 \right) \gt 4.5 \).
Graph your solution on a number line.
\( x \lt - 3.75 \)
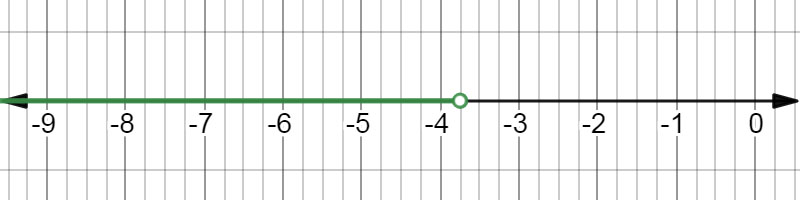
The inequality \( x \lt - 3.75 \) on a number line.
If you need help arriving at this answer, click the Solution button.
Step 1: Apply the distributive property as needed. |
\( - 1.5\left( 2x + 4.5 \right) \gt 4.5 \) \( - 3x - 6.75 \gt 4.5 \) |
Step 2: Solve using inverse operations and the properties of inequality. |
Use the addition property of inequality and then the division property of inequality. Remember to reverse the inequality sign when needed. \( - 3x - 6.75 \gt 4.5 \) \( - 3x \gt 11.25 \) \( x \lt - 3.75 \) |
Step 3: Graph the solution on a number line. |

The inequality \( x \lt - 3.75 \) on a number line. |
Step 4: Check your shading. |
Choose any value that is in the shaded area. Substitute \( x = - 4 \). \( - 1.5\left( 2( - 4) + 4.5 \right) \gt 4.5 \) \( - 1.5\left( - 8 + 4.5 \right) \gt 4.5 \) \( - 1.5\left( - 3.5 \right) \gt 4.5 \) \( 5.25 \gt 4.5 \) |
