Are you ready to take this lesson's quiz? The questions below will help you find out. Make sure you understand why each correct answer is correct—if you don't, review that part of the lesson.
Which is the BEST next step for solving the inequality shown?
\( 4x + 5\left( x + 6 \right) - 10 \lt 9 \)
\( 4x + 5x + 30 - 10 \lt 9 \)
- Combine the like terms on the left-hand side of the inequality.
- Subtract 30 from both sides of the inequality.
- Move all the variable terms to the right-hand side of the inequality.
- Add 10 to both sides of the inequality.
Before using the properties of inequality, you should combine the like terms on the left-hand side.
There are like terms on the left-hand side of the inequality. What can you do with those?
There are like terms on the left-hand side of the inequality. What can you do with those?
There are like terms on the left-hand side of the inequality. What can you do with those?
Which graph represents the solution of \( 3\left( x - 1 \right) \leq x + 4(x - 3) \)?
-

The inequality \( x \leq 2 \) on a number line.
-
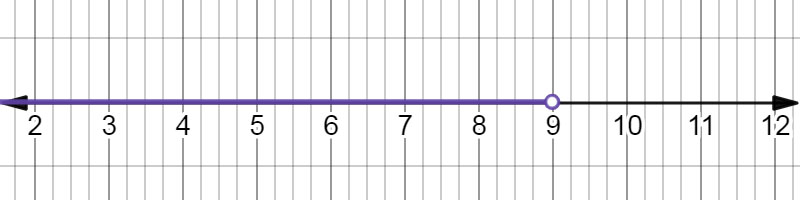
The inequality \( x \lt 9 \) on a number line.
-
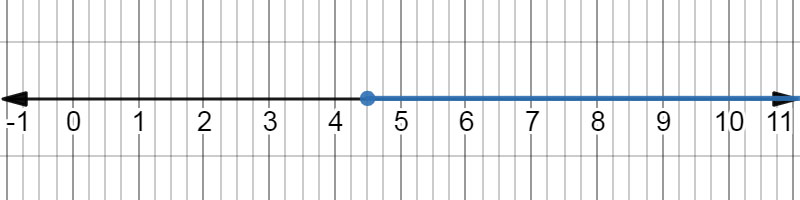
The inequality \( x \geq 4.5 \) on a number line.
-

The inequality \( x \gt - 2 \) on a number line.
Start solving this inequality by applying the distributive property on both sides of the inequality.
Start solving this inequality by applying the distributive property on both sides of the inequality. The graph of the solution will have a closed circle.
Apply the distributive property to both sides of the inequality, and then collect all the variable terms on one side and the constant terms on the other. Use the properties of inequality and inverse operations to finish out the problem and create the graph. \( 3\left( x - 1 \right) \leq x + 4\left( x - 3 \right) \) \( 3x - 3 \leq x + 4x - 12 \) \( 3x - 3 \leq 5x - 12 \) \( 3x - 3x - 3 \leq 5x - 3x - 12 \) \( - 3 \leq 2x - 12 \) \( - 3 + 12 \leq 2x - 12 + 12 \) \( 9 \leq 2x \) \( \frac{9}{2} \leq \frac{2}{2}x \) \( 4.5 \leq x \)
Start solving this inequality by applying the distributive property on both sides of the inequality. The graph of the solution will have a closed circle.
Solve \( - 2x \leq 3(x - 5) \).
- \( x \gt - 3 \)
- \( x \gt 3 \)
- \( x \geq - 3 \)
- \( x \geq 3 \)
Apply the distributive property to the right-hand side of the inequality, and then collect all the variable terms on one side and the constant terms on the other.
Apply the distributive property to the right-hand side of the inequality, and then collect all the variable terms on one side and the constant terms on the other.
Apply the distributive property to the right-hand side of the inequality, and then collect all the variable terms on one side and the constant terms on the other.
Apply the distributive property to the right-hand side of the inequality, and then collect all the variable terms on one side and the constant terms on the other. Remember that you reverse the direction of the inequality when dividing by a negative number. \( - 2x \leq 3\left( x - 5 \right) \) \( - 2x \leq 3x - 15 \) \( - 2x - 3x \leq 3x - 15 - 3x \) \( - 5x \leq - 15 \) \( \frac{- 5}{- 5}x \geq \frac{- 15}{- 5} \) \( x \geq 3 \)
Summary
Questions answered correctly:
Questions answered incorrectly:
