You have learned how to solve inequalities using the distributive property and collecting like terms. This process is similar to the one you learned when you solved equations. For example:
An amusement park security team wants to upgrade their camera system so that each camera has a wider field of vision. They are deciding between two different systems. The cameras offered by Rabbit Security have a maximum field of vision described by the inequality:
\( x + 2\left( x - 105 \right) \leq - x + 210 \)
In this equality, the variable \( x \) represents the camera's maximum field of vision, in degrees.
What is the field of vision of the camera manufactured by Rabbit Security?

The basic steps for solving inequalities that have variables on both sides of the inequality are shown in the table below. Click each step to see it applied to the example.
Distribute on the left-hand side of the inequality. \( x + 2\left( x - 105 \right) \leq - x + 210 \) \( x + 2x - 210 \leq - x + 210 \) |
|
The left-hand side of the inequality has like terms to collect. \( x + 2x - 210 \leq - x + 210 \) \( 3x - 210 \leq - x + 210 \) |
|
Collect the variable terms on the left-hand side of the inequality to keep the coefficient positive. \( 3x \color{#A80000}{+ x} - 210 \leq - x \color{#A80000}{+ x} + 210 \) \( 4x - 210 \leq 210 \) \( 4x - 210 \color{#A80000}{+ 210} \leq 210 \color{#A80000}{+ 210} \) \( 4x \leq 420 \) |
|
Apply the division property of inequality. \( \frac{4x}{\color{#A80000}{\bcancel{4}}} \leq \frac{420}{\color{#A80000}{\bcancel{4}}} \) \( x \leq 105{^\circ} \) |
|
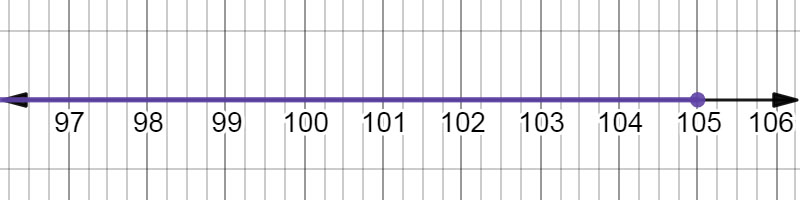
The inequality \( x \leq 105 \) on a number line. |
|
Choose any value in the shaded area. Substitute \( x = 100 \) \( (100) + 2\left( (100) - 105 \right) \leq - (100) + 210 \) \( 100 + 2\left( - 5 \right) \leq - 100 + 210 \) \( 100 - 10 \leq - 100 + 210 \) \( 90 \leq 110 \) |
Question
The solution to the inequality in the example is \( x \leq 105{^\circ} \). What does this tell us about the cameras offered by Rabbit Security?
Since the variable \( x \) represents the camera's maximum field of vision, in degrees, this means that cameras offered by Rabbit Security have a maximum field of vision of \( 105{^\circ} \).
How well can you solve inequalities using the distributive property and collecting like terms? Use the activity below to practice. Solve the inequality that appears on each tab. Then check your answer.
Solve \( 2\left( x + \frac{1}{2} \right) \gt x \).
Graph your solution on a number line.
\( - 1 \lt x \)

The inequality \( - 1 \lt x \) on a number line.
If you need help arriving at this answer, click the Solution button.
Step 1: Use the distributive property, if needed. |
Distribute on the left-hand side of the inequality. \( 2\left( x + \frac{1}{2} \right) \gt x \) \( 2x + 1 \gt x \) |
Step 2: Collect the like terms on each side of the inequality, if needed. |
There are no like terms to combine on either side. |
Step 3: Use the properties of inequality to collect all the variable terms on one side of the inequality and all the constant terms on the other side. |
\( 2x + 1 \gt x \) \( 2x \color{#A80000}{- 2x} + 1 \gt x \color{#A80000}{- 2x} \) \( 1 \gt - x \) |
Step 4: Use inverse operations and the properties of inequality to finish solving. |
Apply the division property of inequality. Remember to reverse the inequality symbol. \( \frac{1}{- 1} \gt - \frac{x}{- 1} \) \( - 1 \lt x \) |
Step 5: Graph your answer on a number line. |

The inequality \( - 1 \lt x \) on a number line. |
Step 6: Check your shading. |
Choose any value in the shaded area. Substitute \( x = 0. \) \( 2\left( \left( 0 \right) + \frac{1}{2} \right) \gt \left( 0 \right) \) \( 2\left( \frac{1}{2} \right) \gt 0 \) \( 1 \gt 0 \) |
Solve \( 30 + 16x \geq 12(2x + 15) \).
Graph your solution on a number line.
\( - 18.75 \geq x \)
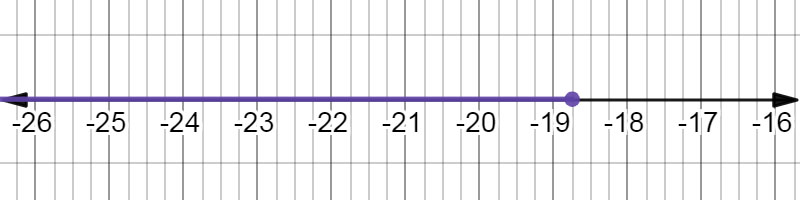
The inequality \( - 18.75 \geq x \) on a number line.
If you need help arriving at this answer, click the Solution button.
Step 1: Use the distributive property, if needed. |
\( 30 + 16x \geq 12\left( 2x + 15 \right) \) \( 30 + 16x \geq 24x + 180 \) |
Step 2: Collect the like terms on each side of the inequality, if needed. |
There are no like terms to combine on either side. |
Step 3: Use the properties of inequality to collect all the variable terms on one side of the inequality and all the constant terms on the other side. |
Collect the variable terms on the right-hand side of the inequality to keep the coefficient positive. \( 30 + 16x \geq 24x + 30 \) \( 30 + 16x \color{#A80000}{- 16x} \geq 24x \color{#A80000}{- 16x} + 180 \) \( 30 \geq 8x + 180 \) \( 30 \color{#A80000}{- 180} \geq 8x + 180 \color{#A80000}{- 180} \) \( - 150 \geq 8x \) |
Step 4: Use inverse operations and the properties of inequality to finish solving. |
Apply the division property of inequality. \( - \frac{150}{\color{#A80000}{8}} \geq \frac{8x}{\color{#A80000}{8}} \) \( - 18.75 \geq x \) |
Step 5: Graph your answer on a number line. |
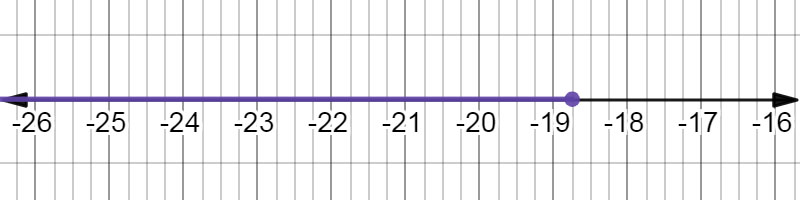
The inequality \( - 18.75 \geq x \) on a number line. |
Step 6: Check your shading. |
Choose any value in the shaded area. Substitute \( x = - 20 \) \( 30 + 16( - 20) \geq 12\left( 2( - 20) + 15 \right) \) \( 30 + 16\left( - 20 \right) \geq 12\left( - 40 + 15 \right) \) \( 30 + 16\left( - 20 \right) \geq 12\left( - 25 \right) \) \( 30 - 320 \geq - 300 \) \( - 290 \geq - 300 \) |
An amusement park security team wants to upgrade their camera system. They are deciding between two different systems. The cameras offered by Strat Security have a maximum field of vision of \( 105{^\circ} \). The maximum field of vision of the cameras offered by Prime Security is described by the inequality: \( 2x + 4\left( x - 42.5 \right) \geq 9x - 425 \), where \( x \) represents the camera's maximum field of vision, in degrees.

What is the maximum field of vision of the cameras offered by Prime Security?
If the security team wants to purchase the cameras with the larger maximum field of vision, which should they choose?
\( 85{^\circ} \geq x \)
The security team should choose the cameras from Strat Security because they have a wider maximum field of vision.
If you need help arriving at this answer, click the Solution button.
Step 1: Use the distributive property, if needed. |
\( 2x + 4\left( x - 42.5 \right) \geq 9x - 425 \) \( 2x + 4x - 170 \geq 9x - 425 \) |
Step 2: Collect the like terms on each side of the inequality, if needed. |
\( \color{#A80000}{2x + 4x} - 170 \geq 9x - 425 \) \( \color{#A80000}{6x} - 170 \geq 9x - 425 \) |
Step 3: Use the properties of inequality to collect all the variable terms on one side of the inequality and all the constant terms on the other side. |
\( 6x - 170 \geq 9x - 425 \) \( - 170 \geq 3x - 425 \) \( 255 \geq 3x \) |
Step 4: Use inverse operations and the properties of inequality to finish solving. |
\( 255 \geq 3x \) \( 85{^\circ} \geq x \) |
Step 5: Graph your answer on a number line. |
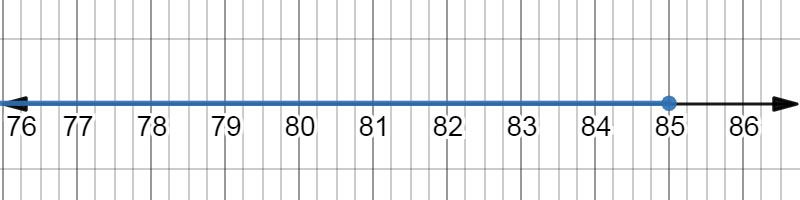
The inequality \( 85 \geq x \) on a number line. |
Step 6: Check your shading. |
Choose any value in the shaded area. Substitute \( x = 84 \) \( 2(84) + 4\left( \left( 84 \right) - 42.5 \right) \geq 9(84) - 425 \) \( 2\left( 84 \right) + 4\left( 41.5 \right) \geq 9\left( 84 \right) - 425 \) \( 168 + 166 \geq 756 - 425 \) \( 334 \geq 331 \) |
Solve \( 1.5\left( 0.5x - 0.5 \right) \leq 0.5x + 2(0.5x - 1.5) \).
Graph your solution on a number line.
\( 3 \leq x \)
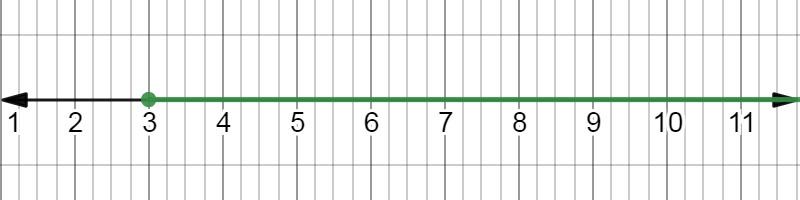
The inequality \( 3 \leq x \) on a number line.
If you need help arriving at this answer, click the Solution button.
Step 1: Use the distributive property, if needed. |
\( 1.5\left( 0.5x - 0.5 \right) \leq 0.5x + 2(0.5x - 1.5) \) \( 0.75x - 0.75 \leq 0.5x + x - 3 \) |
Step 2: Collect the like terms on each side of the inequality, if needed. |
\( 0.75x - 0.75 \leq \color{#A80000}{0.5x + x} - 3 \) \( 0.75x - 0.75 \leq \color{#A80000}{1.5x} - 3 \) |
Step 3: Use the properties of inequality to collect all the variable terms on one side of the inequality and all the constant terms on the other side. |
\( 0.75x - 0.75 \leq 1.5x - 3 \) \( - 0.75 \leq 0.75x - 3 \) \( 2.25 \leq 0.75x \) |
Step 4: Use inverse operations and the properties of inequality to finish solving. |
\( 2.25 \leq 0.75x \) \( 3 \leq x \) |
Step 5: Graph your answer on a number line. |

The inequality \( 3 \leq x \) on a number line. |
Step 6: Check your shading. |
Choose any value in the shaded area. Substitute \( x = 4 \) \( 1.5\left( 0.5(4) - 0.5 \right) \leq 0.5(4) + 2(0.5(4) - 1.5) \) \( 1.5\left( 2 - 0.5 \right) \leq 0.5\left( 4 \right) + 2\left( 2 - 1.5 \right) \) \( 1.5\left( 1.5 \right) \leq 0.5\left( 4 \right) + 2\left( 0.5 \right) \) \( 2.25 \leq 2 + 1 \) \( 2.25 \leq 3 \) |
Tayah is trying to decide which food line to join. The line for veggie burgers is represented by the inequality: \( - 5w - 1 \lt - 2(3w - 4) \), where the variable \( w \) represents the maximum wait time, in minutes, to order.

If Tayah has 10 minutes to wait, does she have enough time to order a burger? Explain.
Yes. Her wait time is less than 9 minutes.
If you need help arriving at this answer, click the Solution button.
Step 1: Use the distributive property, if needed. |
\( - 5w - 1 \lt - 2(3w - 4) \) \( - 5w - 1 \lt - 6w + 8 \) |
Step 2: Collect the like terms on each side of the inequality, if needed. |
There are no like terms to combine on either side. |
Step 3: Use the properties of inequality to collect all the variable terms on one side of the inequality and all the constant terms on the other side. |
\( - 5w - 1 \lt - 6w + 8 \) \( w - 1 \lt 8 \) \( w \lt 9 \) |
Step 4: Use inverse operations and the properties of inequality to finish solving. |
The inequality was solved in the previous step. |
Step 5: Graph your answer on a number line. |
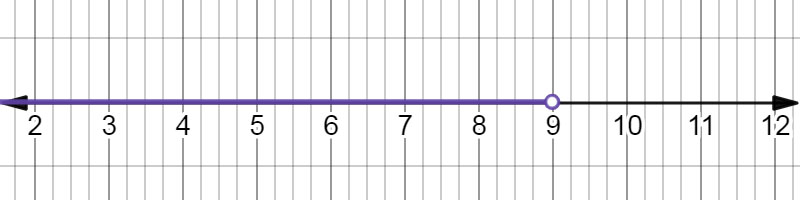
The inequality \( x \lt 9 \) on a number line. |
Step 6: Check your shading. |
Choose any value in the shaded area. Substitute \( x = 8 \) \( - 5(8) - 1 \lt - 2(3(8) - 4) \) \( - 5\left( 8 \right) - 1 \lt - 2\left( 24 - 4 \right) \) \( - 5\left( 8 \right) - 1 \lt - 2\left( 20 \right) \) \( - 40 - 1 \lt - 40 \) \( - 41 \lt - 40 \) |
