Sledding Fun!
Let’s watch a video about partitioned number lines.
Goal:
Goal:
Caleb is going sledding! How high can he jump in his sled? Click on the video below to find out.
Whoa! Did you see that? Caleb is sledding down this hill. I wonder how far he can jump. Let’s find out!
One, two, three, go, Caleb! Caleb jumped three sixths of a foot. Let’s record that fraction on a number line.
We’ll need to use this rectangle first. The denominator is 6, so let’s partition the rectangle into 6 equal parts. The numerator is 3, so we’ll color in 3 of the parts. Perfect! Now let’s start labeling. 0 is here, and 1 is here.
Can you label the fractions? Zero sixths, one sixth, two sixths, three sixths, four sixths, five sixths, and six sixths. Remember, Caleb jumped three sixths of a foot, so our dot goes right here.
Caleb’s headed down the hill again. This time he jumped five eighths of a foot. Nice one, Caleb! I wonder if we can find five eighths on a number line? Let’s start with this rectangle. Do you know why it’s partitioned into 8 equal parts? Yes! It’s because the denominator is 8. Color in 5 parts, and line up the number line with the rectangle. Great! Let’s label! Here’s five eighths.
Caleb has time for one more jump. Go, Caleb! Wow, he jumped two halves of a foot! Let’s find that fraction on a number line.
How many parts will we need in this rectangle? That’s right, 2! 0 goes at one end, and 1 goes at the other end. What fraction goes here? Yes, zero halves. What about here? One half! And here? Two halves! Two halves is a whole because it takes up the entire number line from 0 to 1.
Nice job jumping, Caleb! Thanks for helping Caleb record his jumps on a number line!
Question:
How many parts should a number line be partitioned into if it is recording \({ \frac{3}{8} }\)?
The number line should be partitioned into 8 equal parts because 8 is the denominator in \({ \frac{3}{8} }\).
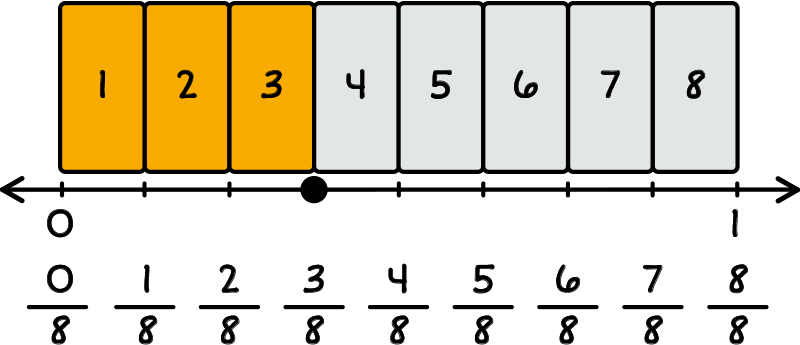
Rectangle with partitioned into 8 equal parts. Number line underneath from 0 to 1 with markers for each part. Markers are labeled \({ \frac{0}{8} }\), \({ \frac{1}{8} }\), \({ \frac{2}{8} }\), \({ \frac{3}{8} }\), \({ \frac{4}{8} }\), \({ \frac{5}{8} }\), \({ \frac{6}{8} }\), \({ \frac{7}{8} }\), \({ \frac{8}{8} }\).