Work through the following flashcards to practice solving problems that involve the tangents of circles. Work out each problem, and then flip the card over to check your work.
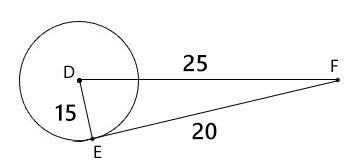
Is \(\mathsf{ \overline {EF} }\) tangent to circle D? Why or why not?
Use the Pythagorean theorem to see if DE is perpendicular to EF. If it is, then EF is a tangent line to circle D.
\(\small\mathsf{ 15^{2}+20^{2}=25^{2} }\)
225 + 400 = 625
625 = 625
The Pythagorean Theorem shows us that triangle DEF is a right triangle. Angle E is a right angle; therefore, EF is a tangent line to circle D with a point of tangency at E.
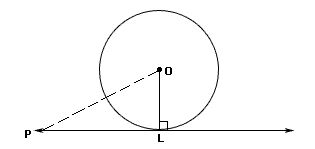
Line PL is tangent to circle O. Line segment OL is perpendicular to line PL. If line segment PL measures 12 cm and OP measures 13 cm, what is the length of OL?
Since PL is tangent to circle O, then we can use the Pythagorean Theorem to find the length of OL.
\(\small\mathsf{ OL^{2}+12^{2}=13^{2} }\)
\(\small\mathsf{ OL^{2}+144=169}\)
\(\small\mathsf{ OL^{2}=25}\)
OL = 5 cm
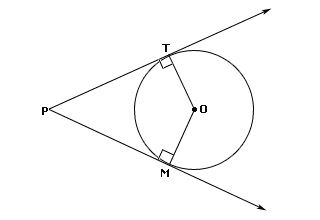
PT and PM are tangent to circle O. If PT measures 5 inches, what is the length of PM?
Since PT and PM are tangent to circle O, they are congruent. If PT has a length of 5 inches, then PM also has a length of 5 inches.
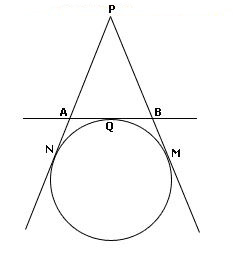
PN and PM are tangent to the circle. If PM equals 45 and PN equals 2x - 10, what is the value of x?
Since PN and PM are tangent to the circle and they originate at an external point, they are congruent. We can write and solve the following equation.
45 = 2x - 10
55 = 2x
x = 27.5
Cards remaining:
