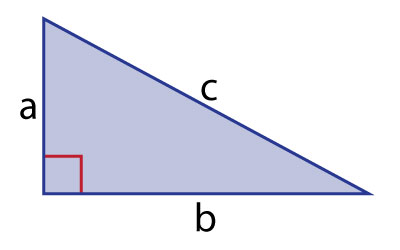
One of the most important theorems in mathematics is called the Pythagorean Theorem. You have used it before and you will use it again in this lesson. Let's review the theorem so that you are ready for this lesson.
Suppose you have a right triangle with two legs measuring 3 cm and 4 cm. What is the length of the hypotenuse?
Use the Pythagorean Theorem to solve this problem:
\(\small\mathsf{ a^{2}+b^{2}=c^{2} }\)
\(\small\mathsf{ 3^{2}+4^{2}=c^{2} }\)
\(\small\mathsf{ 9+16=c^{2} }\)
\(\small\mathsf{ 25=c^{2} }\)
c = 5 cm
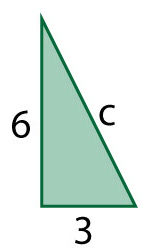
Find the missing hypotenuse of the right triangle above. Round your answer to two decimal places.
Use the Pythagorean Theorem to solve the problem.
\(\small\mathsf{ a^{2}+b^{2}=c^{2} }\)
\(\small\mathsf{6^{2}+3^{2}=c^{2} }\)
\(\small\mathsf{36+9=c^{2} }\)
\(\small\mathsf{45=c^{2} }\)
c\(\mathsf{\approx {} }\)6.71
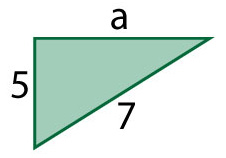
Find the missing side of the right triangle above. Round your answer to two decimal places.
Use the Pythagorean Theorem to solve the problem.
\(\small\mathsf{ a^{2}+b^{2}=c^{2} }\)
\(\small\mathsf{ a^{2}+5^{2}=7^{2}}\)
\(\small\mathsf{ a^{2}+25=49}\)
\(\small\mathsf{a^{2}=24}\)
a \(\mathsf{\approx {} }\)4.90
Cards remaining:
