How is congruence related to other types of line relationships, such as perpendicular lines? The key to answering this question is to think back to what you learned about the perpendicular bisector line. Use the slides below to see how these two concepts are related.
|
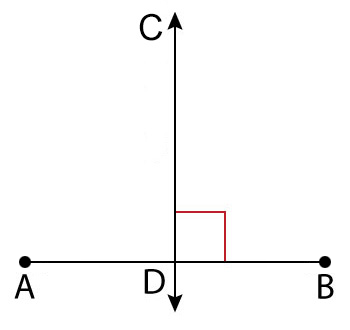
Line CD is a perpendicular bisector of the segment AB. Can you name two segments that are congruent in the diagram? The two line segments AD and DB are congruent because the perpendicular bisector divides segment AB into two equal halves. Those two halves are the same shape and the same size.
Looking at the same diagram from the previous slide, what can you say about the two angles formed by the perpendicular bisector line? m∠CDA = m∠CDB because both are 90 degrees. Also, since the sum of the measures equals 180 degrees, they are supplementary angles. Because they have exactly the same measures, they are congruent. Notice when we talk about the measure of congruent angles, we use an equal sign (=). When we talk about angles themselves, we use the congruent sign (\(\small\mathsf{ \cong }\)). Remember that measures are equal (m∠CDA = m∠CDB) and segments or angles are congruent (\(\small\mathsf{ \overline{AD} \cong \overline{BD} }\) or \(\small\mathsf{ ∠CDA \cong ∠CDB }\)).
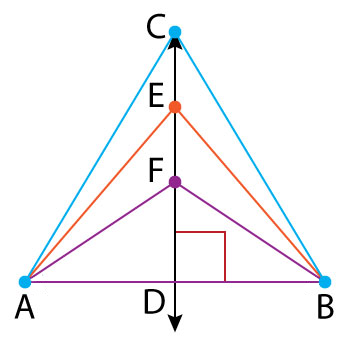
What if we drew segments AC and CB to form a triangle from the perpendicular line bisecting segment AB? Could you say that segments AC and CB are congruent? Why or why not? If you said yes, you are correct! \(\small\mathsf{ \overline{CA} }\) is congruent to \(\small\mathsf{ \overline{CB} }\)
(\(\small\mathsf{ \overline{CA} \cong \overline{CB} }\)) because of the Perpendicular Bisector Theorem, which says: If a point is on the perpendicular bisector of a segment, then it is equidistant from the endpoints of the segment. Since point C is on the perpendicular bisector of segment AB, then point C is equidistant from points A and B. Any point that is on the perpendicular bisector will be equidistant from the endpoints of \(\small\mathsf{ \overline{AB} }\). So, the segments AC and CB will be of equal length.
Let's summarize what we've learned about the properties of a perpendicular bisector. 1) \(\small\mathsf{ \overline{AD} \cong \overline{DB} }\) because a perpendicular bisector cuts a segment into two equal halves.
2) m∠CDA = m∠CDB because both are right angles measuring exactly 90 degrees. 3) Segments formed by any point on the perpendicular bisector and both endpoints (A and B) will be congruent segments. |