The questions on this page are similar to ones you will see on this lesson's quiz. Answer all of these questions, and read the feedback carefully. If you don't understand why one of your answers was incorrect, review that part of this lesson.
A line that intersects another line at a right angle is what type of line?
- equidistant
- skew
- parallel
- perpendicular
A perpendicular line intersects another line at a 90 degree angle.
A perpendicular line intersects another line at a 90 degree angle.
A perpendicular line intersects another line at a 90 degree angle.
A perpendicular line intersects another line at a 90 degree angle.
Given \(\mathsf{\overleftrightarrow{CP} }\) is a perpendicular bisector of \(\mathsf{ \overline {AB} }\) in the picture. What can be said about AC and BC in the picture below?
- \(\mathsf{ \overline {AC} \cong \overline {AP}}\) and \(\mathsf{ \overline {BC} \cong \overline {BP} }\)
- AC + BC = CP
- \(\mathsf{ \overline {AC} \cong \overline {BC}}\)
- AC is longer than BC
Segments \(\mathsf{ \overline {AC} }\) and \(\mathsf{ \overline {BC} }\) are congruent.
Segments \(\mathsf{ \overline {AC} }\) and \(\mathsf{ \overline {BC} }\) are congruent.
Segments \(\mathsf{ \overline {AC} }\) and \(\mathsf{ \overline {BC} }\) are congruent.
Segments \(\mathsf{ \overline {AC} }\) and \(\mathsf{ \overline {BC} }\) are congruent.
Why is \(\mathsf{ \overline {CP} }\) in the picture not a perpendicular bisector?
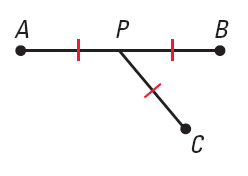
- \(\mathsf{ \overline {CP} }\) is slanted towared the line \(\mathsf{ \overline {BP} }\)
- \(\mathsf{ \overline {CP} }\) does not intersect \(\mathsf{ \overline {AB} }\) at a right angle.
- \(\mathsf{ \overline {CP} }\) is congruent to \(\mathsf{ \overline {AB} }\)
- \(\mathsf{ \overline {AB} }\) is parallel to \(\mathsf{ \overline {BC} }\)
\(\mathsf{ \overline {CP} }\) is does not intersect \(\mathsf{ \overline {AB} }\) at a right angle and thus is not perpendicular.
\(\mathsf{ \overline {CP} }\) is does not intersect \(\mathsf{ \overline {AB} }\) at a right angle and thus is not perpendicular.
\(\mathsf{ \overline {CP} }\) is does not intersect \(\mathsf{ \overline {AB} }\) at a right angle and thus is not perpendicular.
\(\mathsf{ \overline {CP} }\) is does not intersect \(\mathsf{ \overline {AB} }\) at a right angle and thus is not perpendicular.
In the picture, which is a perpendicular bisector?
- \(\mathsf{ \overline {GJ} }\)
- \(\mathsf{ \overline {MK} }\)
- \(\mathsf{ \overline {HK} }\)
- \(\mathsf{ \overline {JH} }\)
\(\mathsf{ \overline {GJ} }\) is the perpendicular bisector because it divides \(\mathsf{ \overline {HK} }\) in half and intersects it at right angles.
\(\mathsf{ \overline {GJ} }\) is the perpendicular bisector because it divides \(\mathsf{ \overline {HK} }\) in half and intersects it at right angles.
\(\mathsf{ \overline {GJ} }\) is the perpendicular bisector because it divides \(\mathsf{ \overline {HK} }\) in half and intersects it at right angles.
\(\mathsf{ \overline {GJ} }\) is the perpendicular bisector because it divides \(\mathsf{ \overline {HK} }\) in half and intersects it at right angles.
Which of the following represents segments that would be considered skew in the picture?
- \(\mathsf{ \overline {HD} }\) and \(\mathsf{ \overline {GH} }\)
- \(\mathsf{ \overline {BE} }\) and \(\mathsf{ \overline {FE} }\)
- \(\mathsf{ \overline {GH} }\) and \(\mathsf{ \overline {BC} }\)
- \(\mathsf{ \overline {AB} }\)and \(\mathsf{ \overline {DE} }\)
Skew lines are noncoplanar and travel in different directions.
Skew lines are noncoplanar and travel in different directions.
Skew lines are noncoplanar and travel in different directions.
Skew lines are noncoplanar and travel in different directions.
Summary
Questions answered correctly:
Questions answered incorrectly:
