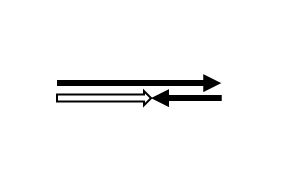
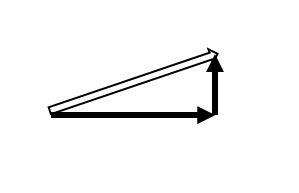
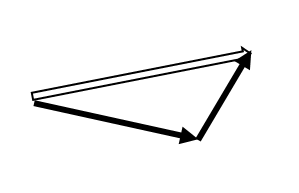
You will have to apply your understanding of adding vectors when you start changing the frame of reference of the motion of an object. Make sure you remember how to add one-dimensional vectors, perpendicular vectors, and vectors in two-dimensions. Click on each image to review each process.
Question
What right-triangle relationships do you need to do vector addition?
You will need the Pythagorean Theorem: \(\small\mathsf{ a^{2}}\)+ \(\mathsf{ b^{2}}\) = \(\mathsf{ c^{2}}\).
You will also need the three trigonometric relationships: \(\small\mathsf{ \sin{\theta} = \frac{opposite}{hypotenuse}}\), \(\small\mathsf{ \cos{\theta} = \frac{adjacent}{hypotenuse}}\), and \(\small\mathsf{ \tan{\theta} = \frac{opposite}{adjacent}}\).