Let's now turn our attention to the river problems. Unlike the car problems, these will deal with velocities that are at an angle to one another, so it's not just an algebraic problem—it's a vector problem. In some cases, you will take a difference and in some cases, you will add. It depends on what arrangement of the equation that you are working with. It really doesn't matter which object is labelled A or B, but the stationary object should always be C. That way your equation always works. If only one of the velocities given in the problem is with respect to the stationary object or observer and one as a relative velocity, it will be an addition problem. If both velocities are given relative to the stationary object or observer, it will be a subtraction problem.
| Problem | Picture | Given/Find | Equation | Solution |
|---|---|---|---|---|
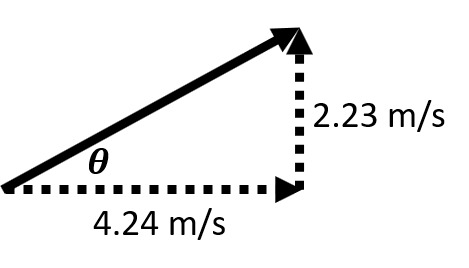
| A river has a current that is 2.23 m/s downstream with respect to the river bank. A motorboat moves across at 4.24 m/s with respect to the river current perpendicularly to the current of the river. What velocity would the boat appear to be moving to a stationary observer on the river bank? |
|
Assign A to the boat, B to the river, and C to the bank: \(\small\mathsf{ \overrightarrow{v_{AB}} = 4.42 \text{ m/s} }\), East \(\small\mathsf{ \overrightarrow{v_{AC}} = ? \text{ m/s} }\) \(\small\mathsf{ \overrightarrow{v_{BC}} = 2.23 \text{ m/s} }\), North |
\(\small\mathsf{ \overrightarrow{v_{AB}} = \overrightarrow{v_{AC}} - \overrightarrow{v_{BC}} }\) \(\small\mathsf{ \overrightarrow{v_{AB}} + \overrightarrow{v_{BC}} = \overrightarrow{v_{AC}} }\) |
\(\small\mathsf{ c^2 = (4.24 \text{ m/s})^2 + (2.23 \text{ m/s})^2 }\) |
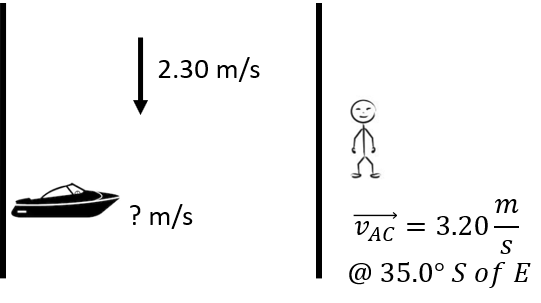
| An observer on the river bank observes a boat travelling at 3.20 m/s at an angle of 35.0° South of East. If the river is moving South at a speed of 2.30 m/s, what is the velocity of the boat relative to the river? |
|
Assign A to the boat, B to the river, and C to the observer: \(\small\mathsf{ \overrightarrow{v_{AB}} =?}\) \(\small\mathsf{ \overrightarrow{v_{AC}} = 3.20 \text{ m/s} }\) directly South \(\small\mathsf{ \overrightarrow{v_{BC}} = 3.20 \text{ m/s} }\) at 325.0° |
\(\small\mathsf{ \overrightarrow{v_{AB}} = \overrightarrow{v_{AC}} - \overrightarrow{v_{BC}} }\) \(\small\mathsf{ \overrightarrow{v_{AB}} = \overrightarrow{v_{AC}} + -\overrightarrow{v_{BC}} }\)> |
Set up the vector addition problem using the opposite of the velocity of the river to the observer:
\(\small\mathsf{\overrightarrow{v_{AC_x}} = (3.20 \text{ m/s}) (\cos325) = 2.62 \text{ m/s} }\) \(\small\mathsf{ c^2 = (2.62 \text{ m/s})^2 + (0.46 \text{ m/s})^2 }\) \(\small\mathsf{ c = \sqrt{7.076 \text{ m}^2 \text{/s}^2} = 2.66 \text{ m/s}}\) \(\small\mathsf{\theta = tan^{-1}(\frac{0.46 \text{ m/s}}{2.62 \text{ m/s}}) = 9.96° }\) The velocity of the boat relative to the river is 2.66 m/s at an angle of 9.96° North of East. |
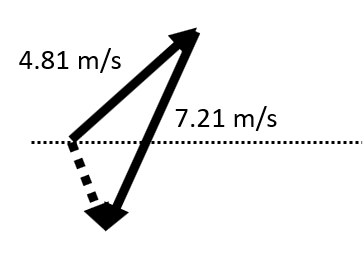
| The velocity of a river current is 4.81 m/s at an angle of 37.3° North of East relative to a stationary observer. The velocity of a motor boat is 7.21 m/s at an angle of 35.4° West of North relative to a stationary observer. What is the river's velocity relative to the boat? |
|
>Assign A to the river, B to the boat, and C to the observer: \(\small\mathsf{ \overrightarrow{v_{AB}} =?}\) \(\small\mathsf{ \overrightarrow{v_{AC}} = 4.81 \text{ m/s} }\) at 37.3° \(\small\mathsf{ \overrightarrow{v_{BC}} = 7.21 \text{ m/s} }\) at 54.6° |
\(\small\mathsf{ \overrightarrow{v_{AB}} = \overrightarrow{v_{AC}} - \overrightarrow{v_{BC}} }\) \(\small\mathsf{ \overrightarrow{v_{AB}} = \overrightarrow{v_{AC}} + -\overrightarrow{v_{BC}} }\)> |
Set up the vector addition problem using the opposite of the velocity of the boat to the observer:
\(\small\mathsf{\overrightarrow{v_{AC_x}} = (4.81 \text{ m/s}) (\cos37.3) = 3.83 \text{ m/s} }\) \(\small\mathsf{ c^2 = (-0.35 \text{ m/s})^2 + (-2.97 \text{ m/s})^2 }\) \(\small\mathsf{ c = \sqrt{8.9434 \text{ m}^2 \text{/s}^2} = 2.99 \text{ m/s}}\) \(\small\mathsf{\theta = tan^{-1}(\frac{-2.97 \text{ m/s}}{-0.35 \text{ m/s}}) = 83.3° }\) The velocity of the river relative to the boat is 2.99 m/s at an angle of 83.3° South of East. |