As you saw in the video, finding relative velocity is actually finding the difference in velocities of two objects as seen by a stationary observer. It is important, though, that you know how to define the frames of reference and what velocity you are looking for. Let's take for example two vehicles that are driving on the same highway in the same direction with a stationary observer on the side of the road.
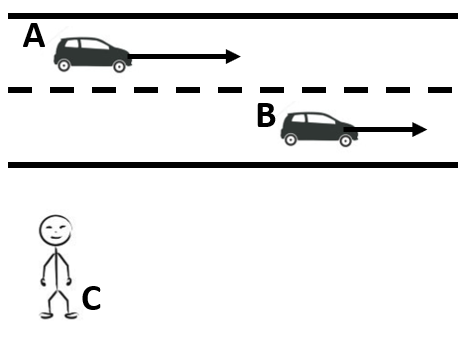
The velocity of the cars relative to the stationary observer would be what the speedometer on the cars show. If you want to know what the relative velocity of one car relative to the other, you need to use vector subtraction.
Relative Velocity
\(\mathsf{ \overrightarrow{v_{AB}} = \overrightarrow{v_{AC}} - \overrightarrow{v_{BC}} }\)
The velocity of A relative to B equals the velocity of A relative to C minus the velocity of B relative to C.
Question
What if you want to find the velocity of B relative to A?
At that point, you will flip the equation around: \(\mathsf{ \overrightarrow{v_{BA}} = \overrightarrow{v_{BC}} - \overrightarrow{v_{AC}} }\)
Question
What if you know the relative velocity and need to find one of the velocities relative to the observer?
Essentially, you can rearrange the equation such that you can find the velocity relative to the observer by adding.
\(\mathsf{ \overrightarrow{v_{AC}} = \overrightarrow{v_{AB}} +\overrightarrow{v_{BC}} }\)
In the video, the river problem was an example of this in application. The problem gave the boat's velocity relative to the river, the velocity of the river with respect to a stationary observer on the bank, and it asked what the velocity of the boat was relative to the stationary observer. It turned out to be a vector addition problem with perpendicular vectors.
