Now we can prove statement 2: If each diagonal bisects a pair of opposite angles, then the parallelogram is a rhombus. If we can do this, then we know our iff postulate is true.
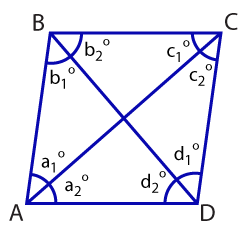
Given: In parallelogram ABCD, AC bisects ∠A and ∠C.
Prove: Parallelogram ABCD is a rhombus.
Click through the tabs below to see how this statement can be proven.
Is it a Rhombus?
Your Turn
Prove that parallelogram ABCD is a rhombus.
| By definition of parallelogram, ∠A = ∠C because opposite sides of a parallelogram are congruent. |
| By definition of bisect, ∠a1 = ∠a2 and ∠c1 = ∠c2. |
| It follows that ∠a1 = ∠c1 and ∠a2= ∠c2 because if two congruent angles are bisected, the angles created by the bisection are congruent as well. |
| By the transitive property ∠a1 = ∠a2 = ∠c1 = ∠c2. |
| Sides opposite congruent angles are congruent as well. Therefore, AB \(\small\mathsf{\cong}\) BC \(\small\mathsf{\cong}\) AD \(\small\mathsf{\cong}\) DC. |
| Because all sides are congruent, parallelogram ABCD is a rhombus. |
Use the previous proof as an example to create your own.
Given: In parallelogram ABCD, BD bisects ∠B and ∠D.
Prove: Parallelogram ABCD is a rhombus.

Create your proof by placing the steps below in the correct order.
|
Because all sides are congruent, parallelogram ABCD is a rhombus.
It follows that ∠b1 = ∠d2 and ∠b2= ∠d1 because if two congruent angles are bisected, the angles created by the bisection are congruent as well.
By definition of bisect, ∠b1 = ∠b2 and ∠d1 = ∠d2.
Sides opposite congruent angles are congruent as well. Therefore, AB \(\small\mathsf{\cong}\) BC \(\small\mathsf{\cong}\) AD \(\small\mathsf{\cong}\) DC.
By the transitive property ∠b1 = ∠b2 = ∠d1 = ∠d2.
By definition of parallelogram, ∠B = ∠D because opposite sides of a parallelogram are congruent.
|
1
2
3
4
5
6
|
Great job! You got them all!
The ones with X's are incorrect. Try again.
