In the exercise on the previous page, you saw that each rhombus diagonal bisects a pair of opposite angles. Here's another special quality of the diagonals—if the diagonals bisect a pair of opposite angles, then the parallelogram is a rhombus. Hence, you have two statements:
1. If a parallelogram is a rhombus, then each diagonal bisects a pair of opposite angles.
2. If each diagonal bisects a pair of opposite angles, then the parallelogram is a rhombus.
Question
You can combine the two statements to create one specific type of postulate. What type of postulate can you create?
if and only if (or iff)
Based on the statements above, you can write the next rhombus postulate: A parallelogram is a rhombus if and only if each diagonal bisects a pair of opposite angles.
Rhombus Postulate
A parallelogram is a rhombus if and only if each diagonal bisects a pair of opposite angles.
Let's go through an example to see how this postulate can be proven.
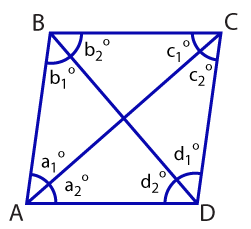
Given: Parallelogram ABCD is a rhombus.
Prove: Diagonal AC bisects ∠A and ∠C. Diagonal BD bisects ∠B and ∠D
Click through the tabs to see how to prove the first statement in our iff postulate.
BD bisects ∠B
BD bisects ∠D
AC bisects ∠C
AC bisects ∠A
Prove BD bisects ∠B.
| Consider △ABD. By definition of rhombus, AB \(\small\mathsf{\cong}\) AD. |
| By definition of isosceles, △ABD is an isosceles triangle because two sides are congruent. |
| Also by definition of isosceles, ∠b1°= ∠d2° because base angles of an isosceles triangle are congruent. |
| By definition of parallel lines, ∠d2°= ∠b2° because they are alternate interior angles. |
| By the transitive property, ∠b1°= ∠d2° = ∠b2°, which implies ∠b1°= ∠b2°. |
| By definition of bisect, BD bisects ∠B. |
Prove BD bisects ∠D.
| Consider △BCD. By definition of rhombus, BC \(\small\mathsf{\cong}\) CD. |
| By definition of isosceles, △BCD is an isosceles triangle because two sides are congruent. |
| Also by definition of isosceles, ∠b2°= ∠d1° because base angles of an isosceles triangle are congruent. |
| By definition of parallel lines, ∠b2°= ∠d2° because they are alternate interior angles. |
| By the transitive property, ∠d1°= ∠b2° = ∠d2°, which implies ∠d1°= ∠d2°. |
| By definition of bisect, BD bisects ∠D. |
You've seen how to prove BD bisects ∠B and ∠D. Use these two proofs as examples to prove that AC bisects ∠C. See if you can write each step before clicking on the table to see if you are correct.
Prove AC bisects ∠C.
| Step 1 | Consider △ABC. By definition of rhombus, AB \(\small\mathsf{\cong}\) BC. |
| Step 2 | By definition of isosceles, △ABC is an isosceles triangle because two sides are congruent. |
| Step 3 | Also by definition of isosceles, ∠a1°= ∠c1° because base angles of an isosceles triangle are congruent. |
| Step 4 | By definition of parallel lines, ∠a1°= ∠c2° because they are alternate interior angles. |
| Step 5 | By the transitive property, ∠c1°= ∠a1° = ∠c2°, which implies ∠c1°= ∠c2°. |
| Step 6 | By definition of bisect, AC bisects ∠C. |
Use what you've learned thus far to prove AC bisects ∠A. Create your proof by placing the steps below in the correct order.
|
By definition of bisect, AC bisects ∠A.
By definition of parallel lines, ∠a1°= ∠c2° because they are alternate interior angles.
By the transitive property, ∠a1°= ∠c2° = ∠a2°, which implies ∠a1°= ∠a2°.
Also by definition of isosceles, ∠a2°= ∠c2° because base angles of an isosceles triangle are congruent.
Prove AC bisects ∠A.
By definition of isosceles, △ACD is an isosceles triangle because two sides are congruent.
Consider △ACD. By definition of rhombus, AD \(\small\mathsf{\cong}\) DC.
|
1
2
3
4
5
6
7 |
You've proven statement 1: If a parallelogram is a rhombus, then each diagonal bisects a pair of opposite angles.
