The graph of a quadratic equation is called a parabola. A parabola can have a maximum or a minimum, depending on which way it opens. The parabola may also have x- and y-intercepts. The maximum or minimum of a parabola is sometimes referred to as an extreme. The extreme is simply the largest or smallest value the quadratic function produces. The word extrema is the plural form of the word extreme.
Similar to a parabola, the graph of a higher-degree polynomial can have minimums, maximums, and intercepts. For higher-degree polynomials, however, you have to determine if the maximum or minimum is a relative extreme or an absolute extreme. Examine the definitions shown.
Relative Extrema
The point(s) on a graph that are the highest or lowest y-values relative to the points close to them on the graph.
Absolute Extrema
The point(s) on a graph that are the highest or lowest y-values of the entire function.
For a polynomial of degree n, its graph will produce, at most, n - 1 relative extrema. The number of absolute extrema depends on the degree of the function. A polynomial of odd degree will have no absolute extrema. A polynomial of even degree will have 0 or an even number of absolute extrema.
In the activity below, you will practice finding the relative and absolute extrema of higher-order polynomial functions.
This is the graph of y=5x3−6x. This is a third-degree polynomial, so it has, at most, 3 - 1 = 2 relative extrema.
There is a relative maximum that occurs between x = -1 and x = 0. There is a relative minimum that occurs between x = 0 and x = 1.
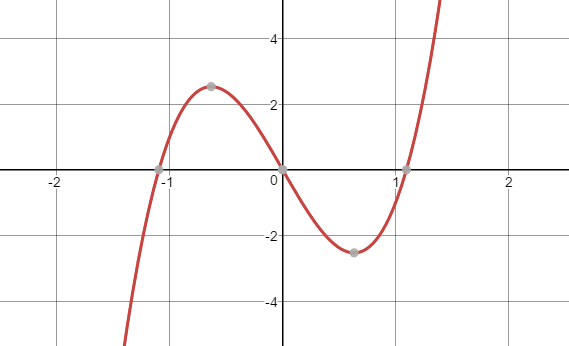
Question
Describe the end behavior of this graph.
This is an odd degree polynomial with a positive leading coefficient. The end behavior is left tail downward, right tail upward.
Since this is an odd degree polynomial, it will not have absolute extrema. This makes sense because the function values reach negative infinity as the x-values become smaller and positive infinity as the x-values become larger, as predicted by the polynomial's end behavior.
Question
Examine the graph. All the roots of the equation are on the graph. What is the degree of the polynomial? Use the graph to state the number of relative extrema and their locations to the best of your ability. Finish by explaining if this polynomial has absolute extrema.
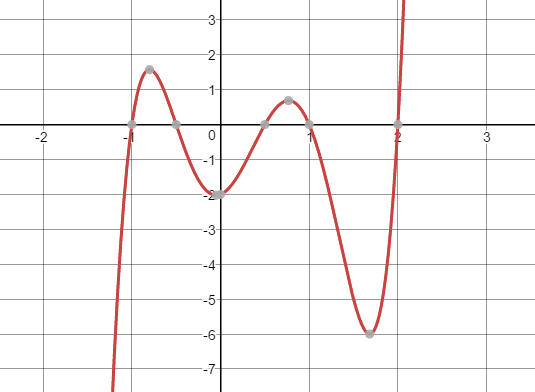
There are five roots on the graph, so this is a 5th degree polynomial. There are, at most, 5 - 1 = 4 relative extrema.
A relative maximum is between x = -1 and x = 0.
A relative minimum at (0, -2).
A relative maximum is between x = 0 and x = 1.
A relative minimum is between x = 1 and x = 2.
Since this is an odd degree polynomial, it will not have absolute extrema.