Now you try using your protractor to measure some angles. Carefully place your protractor against your computer or tablet screen to find the degree of each angle shown in the tabs below. After you have identified the degree of each angle, click the Answer button to check your work.
Angle 1
Angle 2
Angle 3
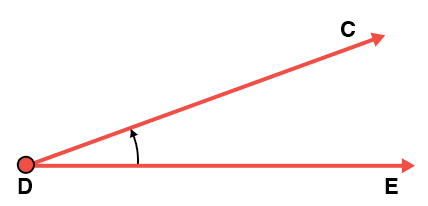

m∠CDE = 20°
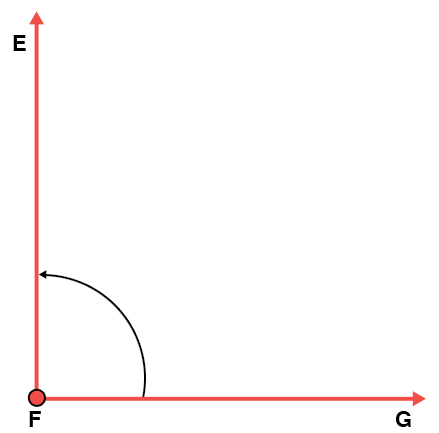

m∠EFG = 90°
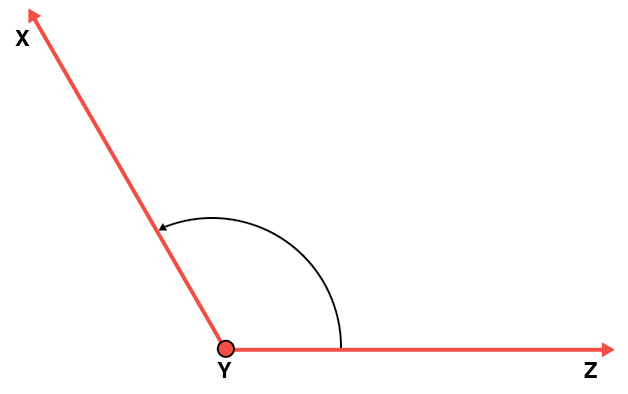

m∠XYZ = 120°
Not every angle you encounter will have a horizontal base like the angles above. When you encounter a tilted angle, you just need to identify the ray to be the angle's base. Often, the direction of the angle is identified for you. Then place the protractor's straight-edge center at the vertex of the angle and line up the straight edge along the ray you've identified as the base.
The example below shows an angle that has been tilted but, like all angles, can still be measured using a protractor.
(Note: This angle was drawn with →BA rotated counterclockwise from →BC, indicating →BC as the initial side.)

