Problem solving with series circuits is a matter of first figuring out the equivalent resistance, then using the equivalent resistance to find the current through the circuit, and then going back to the original resistance in each resistor to find the voltage drop across each one.
| Problem | Picture | Given/Find | Equation | Solution |
|---|---|---|---|---|
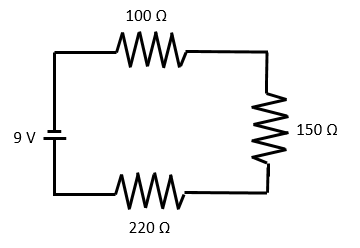
| A 220 Ω, a 150 Ω, and a 100 Ω resistor were connected in series along with a 9.0 V battery. What is the equivalent resistance of the circuit? |
|
\(\mathsf{ R_1 = 220 \text{ Ω}}\) \(\mathsf{ R_2 = 150 \text{ Ω}}\) \(\mathsf{ R_3 = 100 \text{ Ω}}\) \(\mathsf{ R_{eq} = ? \text{ Ω}}\) |
\(\mathsf{ R_{eq} = R_1 + R_2 + R_3 }\) | \(\mathsf{ R_{eq} = 220 \text{ Ω} + 150 \text{ Ω} + 100 \text{ Ω}}\) \(\mathsf{ R_{eq} = 470 \text{ Ω}}\) |
| A 220 Ω, a 150 Ω, and a 100 Ω resistor were connected in series along with a 9.0 V battery. How much current is flowing through each resistor? |
|
\(\mathsf{ R_{eq} = 470 \text{ Ω}}\) \(\mathsf{ V = 9.0 \text{ V}}\) \(\mathsf{ I = ? \text{ A} }\) |
\(\mathsf{ I = \frac{V}{R_{eq}} }\) | \(\mathsf{ I = \frac{9.0 \text{ V}}{470 \text{ Ω}} }\) \(\mathsf{ I = 0.019 \text{ A} }\) |
| A 220 Ω, a 150 Ω, and a 100 Ω resistor were connected in series along with a 9.0 V battery. What is the voltage drop across each resistor? |
|
\(\mathsf{ R_1 = 220 \text{ Ω}}\) \(\mathsf{ R_2 = 150 \text{ Ω}}\) \(\mathsf{ R_3 = 100 \text{ Ω}}\) \(\mathsf{ I = 0.019 \text{ A} }\) \(\mathsf{ V_1 = ? \text{ V} }\) \(\mathsf{ V_2 = ? \text{ V} }\) \(\mathsf{ V_3 = ? \text{ V} }\) |
\(\mathsf{ V = IR }\) | \(\mathsf{ V_1 = (0.019 \text{ A})(220 \text{ Ω}) = 4.2 \text{ V}}\) \(\mathsf{ V_2 = (0.019 \text{ A})(150 \text{ Ω}) = 2.9 \text{ V}}\) \(\mathsf{ V_3 = (0.019 \text{ A})(100 \text{ Ω}) = 1.9 \text{ V}}\) \(\mathsf{ V_{total} = 4.2 \text{ V} + 2.9 \text{ V} + 1.9 \text{ V} = 9.0 \text{ V}}\) |