Let’s say you have a series circuit connected to a 6-volt battery. You add to the circuit, one at a time, a fan with resistance of 3 ohms, a light bulb with resistance of 1 ohm, and an electric clock with resistance of 2 ohms.



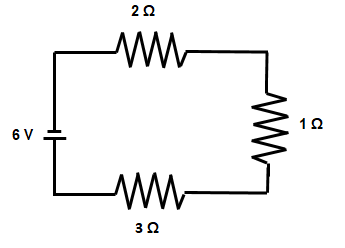
You can answer several questions regarding this simple series circuit: the equivalent resistance, the current through the whole circuit and through each resistor, and the voltage drop across each resistor. Click through the slides below to see each step.
|
Find the Equivalent Resistance Add up each of the resistances of the individual resistors to find the equivalent resistance of the circuit. \(\mathsf{ R_{\text{series equivalent}} = R_1 + R_2 + R_3 }\) \(\mathsf{ R_{\text{series equivalent}} = 3 \text{ Ω} + 1 \text{ Ω} + 2 \text{ Ω} }\) \(\mathsf{ R_{\text{series equivalent}} = 6 \text{ Ω} }\) Find the Current Through the Whole Circuit Find the current through the whole circuit using Ohm's Law and the equivalent resistance. \(\mathsf{ I = \frac{V}{R_{eq}} }\) \(\mathsf{ I = \frac{6 \text{ V}}{6 \text{ Ω}} }\) \(\mathsf{ I = 1 \text{ A} }\) Note, in a series circuit, the current through each resistor is the SAME as it is through the whole circuit. Find the Voltage Drop Across Each Resistor To find the voltage drop across each resistor, use the resistance of the individual resisitor and the current through each resistor and solve for V using Ohm's Law. \(\mathsf{ V = IR }\) \(\mathsf{ V_1 = (1 \text{ A})(3 \text{ Ω}) = 3 \text{ V}}\) \(\mathsf{ V_2 = (1 \text{ A})(1 \text{ Ω}) = 1 \text{ V}}\) \(\mathsf{ V_3 = (1 \text{ A})(2 \text{ Ω}) = 2 \text{ V}}\) Note, the sum of the voltage drop across all three resistors equals the total potential difference given by the power source (6 V). |
