Ring Toss Fractions
Let’s watch a video about creating fraction models!
Goal:
Goal:
Madelyn is playing a ring toss game! Let’s watch as she creates equivalent fractions with the rings.
Madelyn is in the backyard playing with her ring toss toy! Go, Madelyn, go!
There are 3 purple rings and 1 white ring on this peg, and there are 6 blue rings and 2 white rings on this peg. Madelyn wants to create partitioned shapes to represent the fraction of rings on each peg.
These squares are the same shape and size. Let’s partition the first square into 4 equal parts to represent the 4 total rings on the first peg, and the second square into 8 equal parts to represent the 8 total rings on the second peg.
The numerators help us know how many parts to color. Let’s color 3 parts for \({ \frac{3}{4} }\), which tells the number of purple rings, \({ \frac{6}{8} }\), which tells us the number of blue rings.
Excellent! Look at these shapes. They prove that \({ \frac{3}{4} }\) and \({ \frac{6}{8} }\) are equivalent fractions because the purple and blue take up the same amount of space in both shapes.
Madelyn is playing more ring toss! Now there are 3 orange rings and 3 white rings on this peg, and 4 yellow rings and 4 white rings on this peg. Madelyn wants to create number lines to represent the fractions for the rings on each peg. Let’s get to work!
We’ll start by drawing 2 number lines, one above the other. Draw an arrow at each end of each number line, and label the lines with 0 and 1. It’s very important that these numbers match so that the number lines are the same size.
Let’s partition the first number line into 6 equal parts and the second number line into 8 equal parts to represent the number of rings on each peg.
Place a dot at \({ \frac{3}{6} }\) on the first number line to show the number of orange rings, and a dot at \({ \frac{4}{8} }\) on the second number line to show the number of yellow rings.
Great job! These number lines prove that \({ \frac{3}{6} }\) and \({ \frac{4}{8} }\) are equivalent fractions because the dots line up.
Thanks for helping Madelyn create models to represent these equivalent fractions!
Which set of number lines shows equivalent fractions? Click the number lines below to find out!
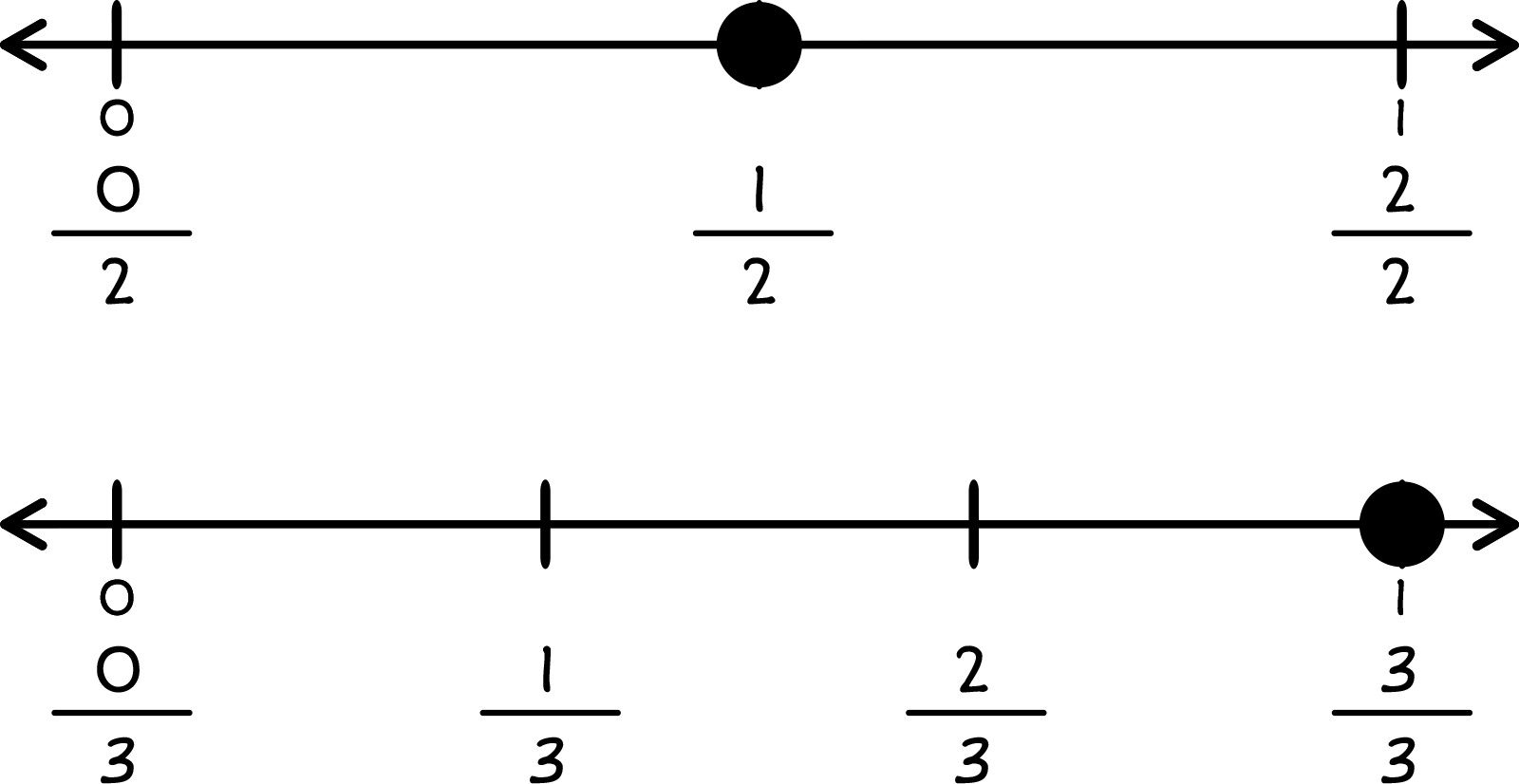
Two number lines.
Top number line from 0 to 1 with 3 marks between. Marks are labeled from \({ \frac{0}{2} }\) to \({ \frac{2}{2} }\) with a dot on \({ \frac{1}{2} }\).
Bottom number line from 0 to 1 with 4 marks between. Marks are labeled from \({ \frac{0}{3} }\) to \({ \frac{3}{3} }\) with a dot on \({ \frac{3}{3} }\).
Two number lines.
Top number line from 0 to 1 with 3 marks between. Marks are labeled from \({ \frac{0}{2} }\) to \({ \frac{2}{2} }\) with a dot on \({ \frac{1}{2} }\).
Bottom number line from 0 to 1 with 4 marks between. Marks are labeled from \({ \frac{0}{3} }\) to \({ \frac{3}{3} }\) with a dot on \({ \frac{3}{3} }\).
Dotted line from the top number line \({ \frac{1}{2} }\) down through the bottom number line. Dotted line from the bottom number line \({ \frac{3}{3} }\) through the top number line. The dots do not match up.
🤔 \({ \frac{1}{2} }\) and \({ \frac{3}{3} }\) are not equivalent fractions because they do not line up.
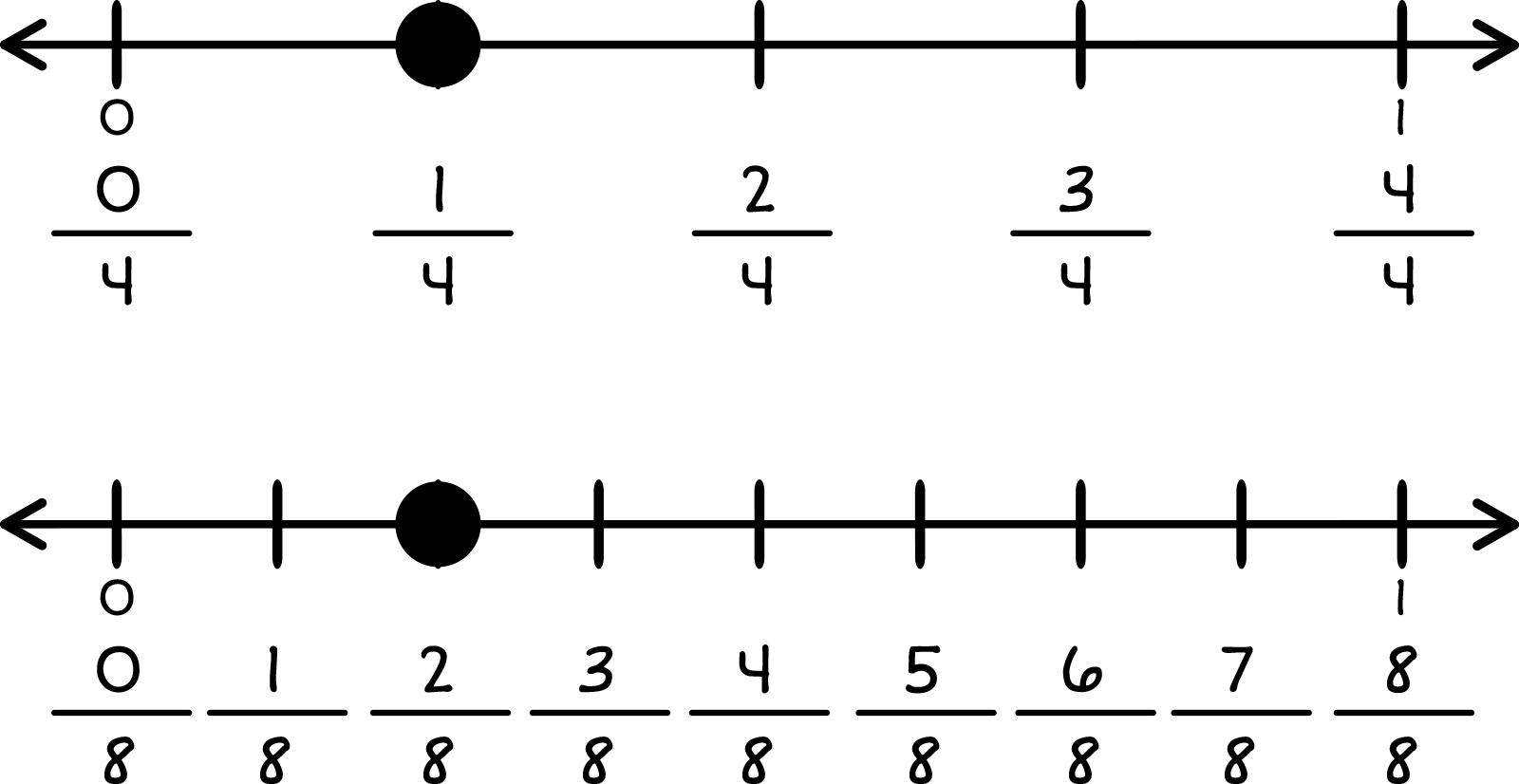
Two number lines.
Top number line line from 0 to 1 with 5 marks between. Marks are labeled from \({ \frac{0}{4} }\) to \({ \frac{4}{4} }\) with a dot on \({ \frac{1}{4} }\).
Bottom number line line from 0 to 1 with 9 marks between. Marks are labeled from \({ \frac{0}{8} }\) to \({ \frac{8}{8} }\) with a dot on \({ \frac{2}{8} }\).
Two number lines.
Top number line line from 0 to 1 with 5 marks between. Marks are labeled from \({ \frac{0}{4} }\) to \({ \frac{4}{4} }\) with a dot on \({ \frac{1}{4} }\).
Bottom number line line from 0 to 1 with 9 marks between. Marks are labeled from \({ \frac{0}{8} }\) to \({ \frac{8}{8} }\) with a dot on \({ \frac{2}{8} }\).
Dotted line from the top number line \({ \frac{1}{4} }\) through the bottom number line \({ \frac{2}{8} }\). The dots match up.
😀 Yes! \({ \frac{1}{4} }\) and \({ \frac{2}{8} }\) are equivalent fractions because they line up.