Where to start?
The best place to start with any problem is setting up your work neatly. Consider the problem:
Introduction
How do you add mixed numbers with like denominators?
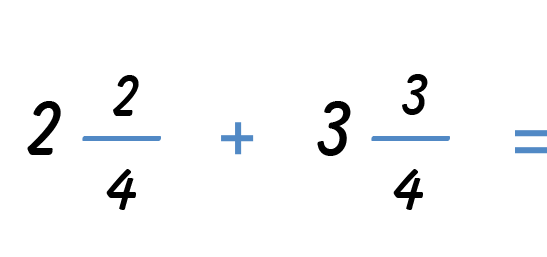
Goal:
Goal:
Sometimes you will need to work with fractions that are a
combination of a whole number and a fraction. These are called
mixed numbers. For example, \(\mathsf{
2\frac{3}{4} }\) is a mixed number because it has both a whole
number (2) and a fraction \(\mathsf{ \frac{3}{4} }\). This
number is between 2 and 3 on the number line.
Adding mixed numbers uses many of the steps that you have learned for adding other fractions. Let’s take a closer look at adding mixed numbers. To start, review the slides to learn how to add mixed numbers with like denominators.
Add the Fractions
When the fractions have like (same) denominators, add them using what you have learned about adding other fractions with like denominators.
1. Keep the denominator the same, and record it in your sum.
2. Add your numerators.
Your fractions are added, and you are ready to add your whole numbers.
Add the Whole Numbers
Adding the whole numbers in a set of mixed numbers is just like adding any other whole numbers. You will use the same strategies you have always used, like this:
2 + 3 = 5.
Simplify the Fraction
When adding whole numbers, you might need to simplify your sum. First evaluate the fraction part of your answer. Look at the fraction sum below; can you make any additional whole groups from this sum?
\(\mathsf{ \frac{5}{4} }\) is more than one whole, which would be \(\mathsf{ \frac{4}{4} }\). When the numerator is larger than the denominator, called an improper fraction, you can make additional whole values.
To do this, subtract the value of a whole, which is the denominator, from the numerator.
In this example you will subtract: 5 – 4 = 1
Record your answer over the denominator.
Now the denominator is less than the numerator. You have simplified the fraction to a whole value. So, in this example, \(\mathsf{ \frac{5}{4} }\) became:
One last step before returning to your whole number: decide if the fraction can be simplified by a common factor. In this example, \(\mathsf{ \frac{1}{4} }\) is already simplified.
Finish It Up!
After simplifying the improper fraction, we get another mixed fraction (\(\mathsf{ \frac{5}{4} }\) became \(\mathsf{ 1\frac{1}{4} }\)). Now you need to add the whole number of this new mixed fraction to the whole number previously calculated. This means we must add the whole numbers 5 and 1:
Put your whole number together with your simplified fraction for your final answer:
Altogether:
Practice makes perfect! Use your understanding of mixed fractions and addition to work through these practice problems. When ready, click each problem to check your answers.
\(\mathsf{ 2\frac{3}{6} + 1\frac{5}{6} = }\)
Add the fractions.
\(\mathsf{ \frac{3}{6} + \frac{5}{6} = \frac{8}{6} }\)
Add the whole numbers.
\(\mathsf{ 2\frac{3}{6} + 1\frac{5}{6} = 3\frac{8}{6} }\)
Simplify the improper fraction to a mixed number.
\(\mathsf{ \frac{8}{6} = 1\frac{2}{6} }\)
Add the whole numbers with the mixed number you created when you added your fractions.
\(\mathsf{ 3 + 1\frac{2}{6} = 4\frac{2}{6} }\)
One last step: the fraction \(\mathsf{ \frac{2}{6} }\) can
be simplified further.
2 and 6 share the GCF of 2. Divide the fraction by the GCF
to simplify.
\begin{align*} \underline{2} \div 2 &= \underline{1} \\ 6 \div 2 &= 3 \end{align*}
So, the final answer is:
\(\mathsf{ 4\frac{1}{3} }\)
\(\mathsf{ 4\frac{5}{7} + 5\frac{2}{7} = }\)
Add the fractions.
\(\mathsf{ \frac{5}{7} + \frac{2}{7} = \frac{7}{7} }\)
Add the whole numbers.
\(\mathsf{ 4\frac{5}{7} + 5\frac{2}{7} = 9\frac{7}{7} }\)
When the numerator and denominator of a fraction are the same, you have 1 whole.
\(\mathsf{ \frac{7}{7} }\) is the same as 1 whole.
So... \(\mathsf{ 9\frac{7}{7} }\) can be simplified to 9 + 1 = 10.
Your final answer is 10.
\(\mathsf{ 3\frac{6}{10} + 5\frac{8}{10} = }\)
Add the fractions.
\(\mathsf{ \frac{6}{10} + \frac{8}{10} = \frac{14}{10} }\)
Add the whole numbers.
\(\mathsf{ 3\frac{6}{10} + 5\frac{8}{10} = 8\frac{14}{10} }\)
Simplify the improper fraction to a mixed number.
\(\mathsf{ \frac{14}{10} = 1\frac{4}{10} }\)
Add the whole numbers with the mixed number you created when you added your fractions.
\(\mathsf{ 8 + 1\frac{4}{10} = 9\frac{4}{10} }\)
One last step: the fraction \(\mathsf{ \frac{4}{10} }\) can
be simplified further.
4 and 10 share the GCF of 2. Divide the fraction by the GCF
to simplify.
\begin{align*} \underline{\hspace{5px}4 \hspace{5px}} \div 2 &= \underline{2} \\ 10 \div 2 &= 5 \end{align*}
So, the final answer is:
\(\mathsf{ 9\frac{2}{5} }\)