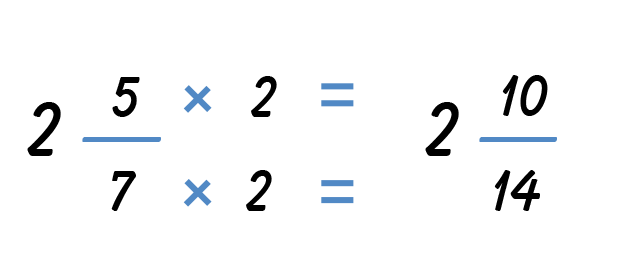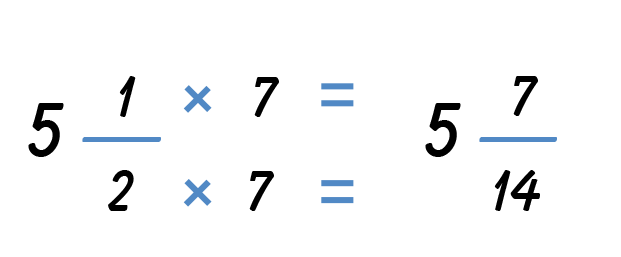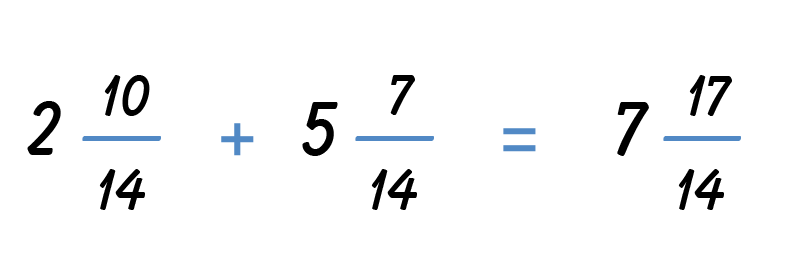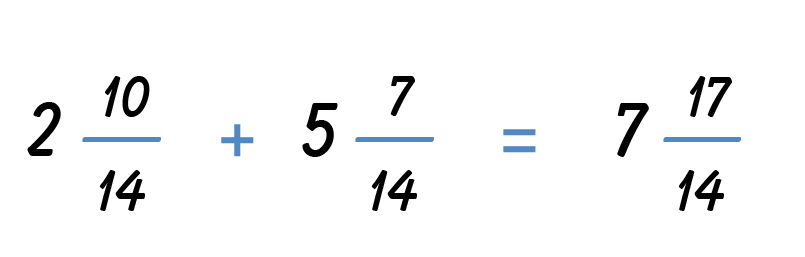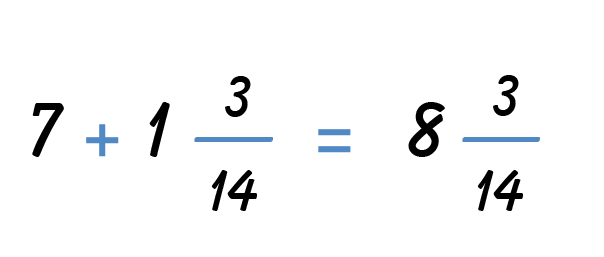Mixed Numbers with Unlike Denominators

Adding mixed numbers with unlike denominators is very similar to adding mixed numbers with like denominators. The biggest difference is that you need to use the LCM to determine the LCD of the two mixed fractions.

Work through the slides to take a closer look at adding mixed numbers with unlike denominators.

Slide: 1 / 5

Getting Started

Consider the problem:

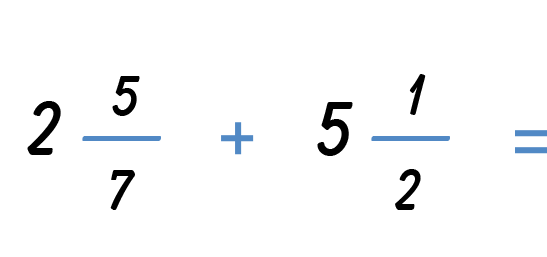
Two and five sevenths plus five and one half equals...

You need a common denominator to add the fractions. Use the LCM to find the LCD, lowest common denominator of the two mixed fractions. Recall that the LCM is the smallest multiple that both numbers have in common.

To identify the LCM, list the multiples of each number until you find a common multiple, like this:
Multiples of 2: 2, 4, 6, 8, 10, 12, 14
Multiples of 7: 7, 14

The LCM of 2 and 7 is 14, which means that the LCD is 14.

Equivalent Fractions

Use the LCD you found to create equivalent fractions. Remember, when creating your equivalent fractions, you must multiply the numerator and denominator of a fraction by the same number.

Two and five sevenths; times the numerator and denominator by two; the sum is two and ten fourteenths.

Five and one half; times the numerator and denominator by seven; the sum is five and seven fourteenths.

Simplify

Simplify if possible.

$\mathsf{ \frac{17}{14} }$ is an improper fraction. You can simplify the improper fraction to a mixed number. First, subtract your denominator from your numerator to make a whole.
17 – 14 = 3.

The new mixed number is:

This means that $\mathsf{ \frac{17}{14} = 1\frac{3}{14} }$

Now, add the new mixed number to the whole number that was already part of your answer (7).

Seven plus one and three fourteenths; the sum equals eight and three fourteenths.

Your final answer is:

Time to practice! You have learned a lot about adding mixed numbers with unlike denominators. Use what you have learned to complete these practice problems. Click each row to check your work.

$\mathsf{ 7\frac{1}{4} + 4\frac{2}{6} = }$

Find the LCD (or LCM).
Multiples of 4: 4, 8, 12, 16
Multiples of 6: 6, 12, 18
LCD of 4 and 6 is 12.

Create equivalent fractions.

$\mathsf{7 \frac{1 \times 3}{4 \times 3} = 7\frac{3}{12} }$

$\mathsf{4 \frac{2 \times 2}{6 \times 2} = 4\frac{4}{12} }$

Add the fractions.

$\mathsf{ \frac{3}{12} + \frac{4}{12} = \frac{7}{12} }$

Add the whole numbers.

$\mathsf{ 7\frac{3}{12} + 4\frac{4}{12} = 11\frac{7}{12} }$

Your final answer is:

$\mathsf{ 11\frac{7}{12} }$

$\mathsf{ 6\frac{4}{9} + 5\frac{3}{6} = }$

Find the LCD.
Multiples of 9: 9, 18, 27
Multiples of 6: 6, 12, 18
LCD of 9 and 6 is 18.

Create equivalent fractions.

$\mathsf{6 \frac{4 \times 2}{9 \times 2} = 6\frac{8}{18} }$

$\mathsf{5 \frac{3 \times 3}{6 \times 3} = 5\frac{9}{18} }$

Add the fractions.

$\mathsf{ \frac{8}{18} + \frac{9}{18} = \frac{17}{18} }$

Add the whole numbers.

$\mathsf{ 6\frac{8}{18} + 5\frac{9}{18} = 11\frac{17}{18} }$

Your final answer is:

$\mathsf{ 11\frac{17}{18} }$

$\mathsf{ 9\frac{3}{4} + 10\frac{4}{5} = }$

Find the LCD.
Multiples of 4: 4, 8, 12, 16, 20, 24
Multiples of 5: 5, 10, 15, 20, 25
LCD of 4 and 5 is 20.

Create equivalent fractions.

$\mathsf{9 \frac{3 \times 5}{4 \times 5} = 9\frac{15}{20} }$

$\mathsf{10 \frac{4 \times 4}{5 \times 4} = 10\frac{16}{20} }$

Add the fractions.

$\mathsf{ \frac{15}{20} + \frac{16}{20} = \frac{31}{20} }$

Add the whole numbers.

$\mathsf{ 9\frac{15}{20} + 10\frac{16}{20} = 19\frac{31}{20} }$

Simplify.

$\mathsf{ \frac{31}{20} }$ is an improper fraction. You can simplify $\mathsf{ \frac{31}{20} }$ to a mixed number.

Subtract: 31 - 20 = 11

This means you can make 1 whole group of 20 with $\mathsf{ \frac{11}{20} }$ left over.

Your new mixed number is:

$\mathsf{ 1\frac{11}{20} }$

So, $\mathsf{ \frac{31}{20} = 1\frac{11}{20} }$ .

Now, add the new mixed number to the whole number that was already part of your answer.

$\mathsf{ 19 + 1\frac{11}{20} = 20\frac{11}{20} }$

Your final answer is:

$\mathsf{ 20\frac{11}{20} }$

Learning Coach — Adding Mixed Numbers

Objectives

Skills Needed

Keywords

Learning Coach Notes

Mixed Numbers with Unlike Denominators

What do you do when the denominators are different?

Getting Started

Equivalent Fractions

Add the Fractions

Add the Whole Numbers

Simplify