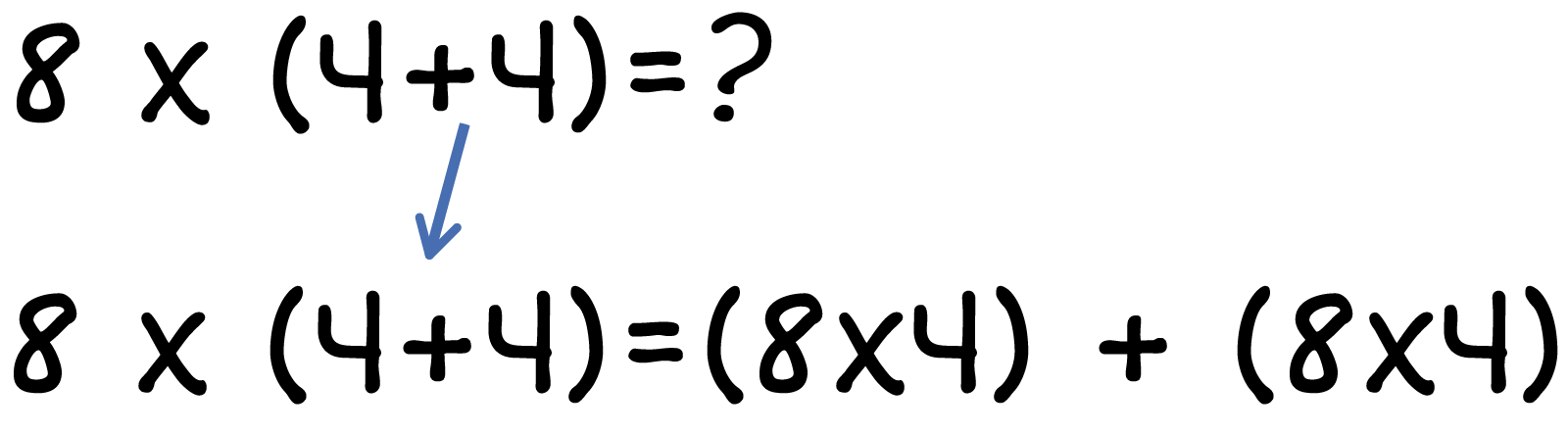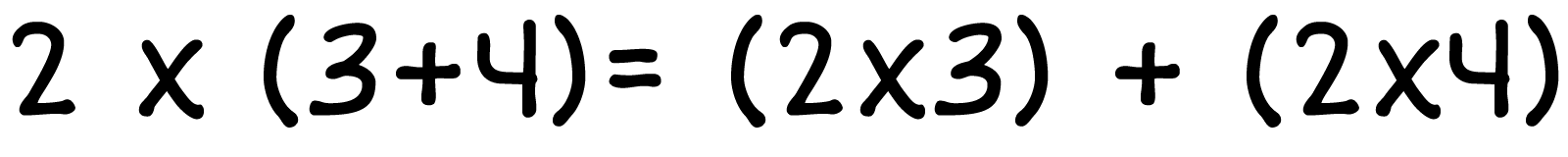Let’s Learn!
How do we use the properties of operations to add and multiply?
Goal:
Goal:

Think About It!
Goal: Define the properties of operations and recognize how to use them for addition and multiplication.

Daniel with two plates of celery each plate has a group of 3 celery sticks and one of four celery sticks.
Daniel is making “ants on a log” snacks. He will use celery sticks, raisins, and nut butter. Daniel has 2 plates of celery sticks. Each plate has a group of 3 sticks and a group of 4 sticks. Daniel wants to know how many sticks he has in all.
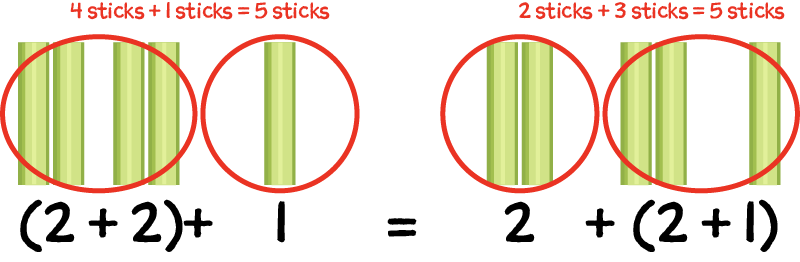
Daniel remembers a new way to write an equation. When we have a situation like the plates of celery, we can create an equation that fits what we need to find.
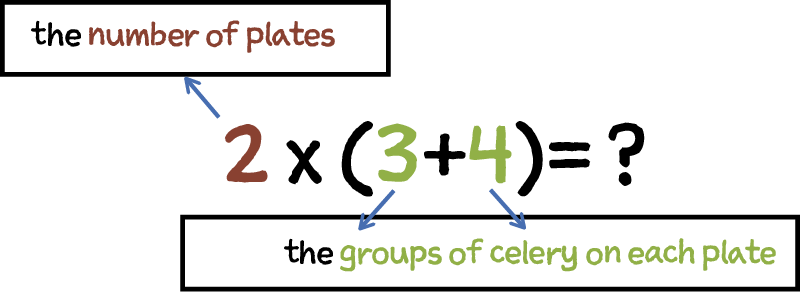
The number of plates pointing to the 2 in the equation.
2×(3+4)=?
3 and 4 are the groups of celery on each plate and points to the label.
How can we help Daniel find the total number of celery sticks with this new type of equation? We can use the properties of operations! The properties of operations are rules about adding or multiplying that help us understand and solve equations. These properties are the identity property, the commutative property, the associative property, and the distributive property. We will use these properties to help us solve different equations.
Question
1. Click the equation that shows the associative property.
- 13+0=13
- 24+45=45+24
- (15+12)+30=15+(12+30)
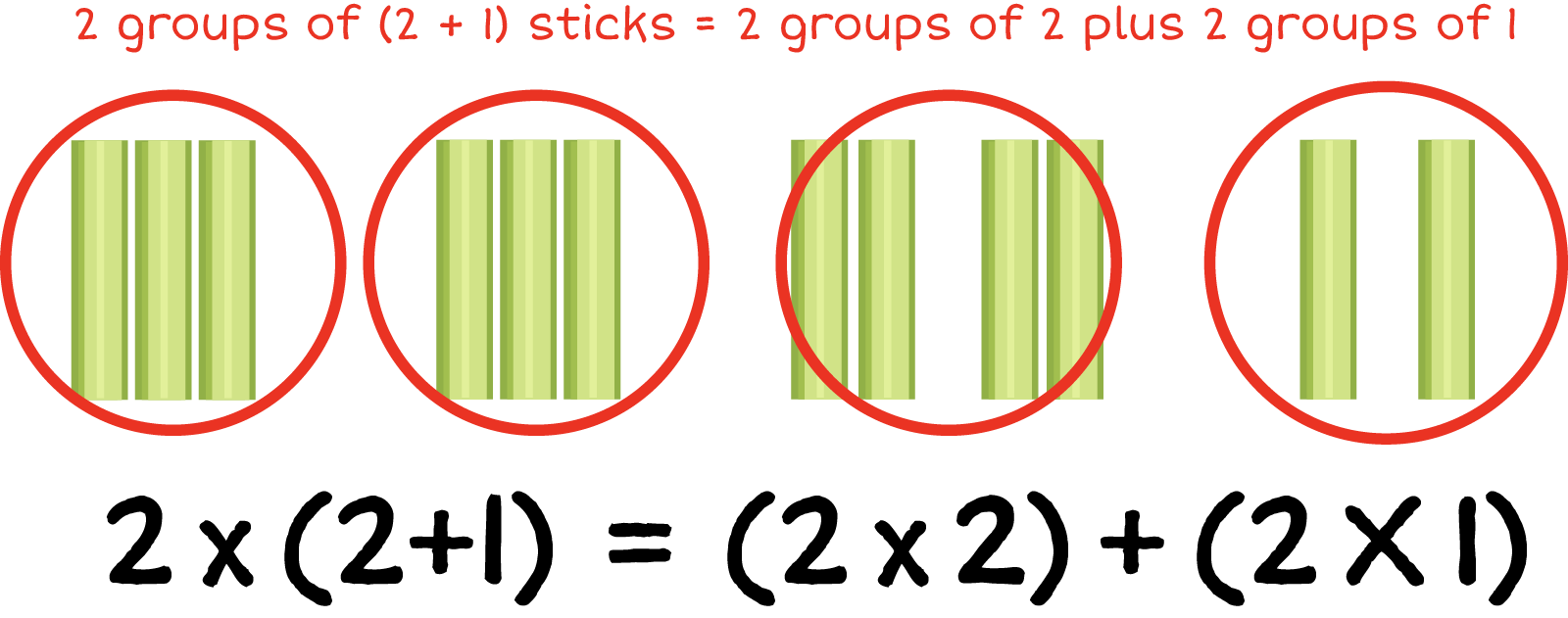
- 3×(4+5)=(3×4)+(3×5)
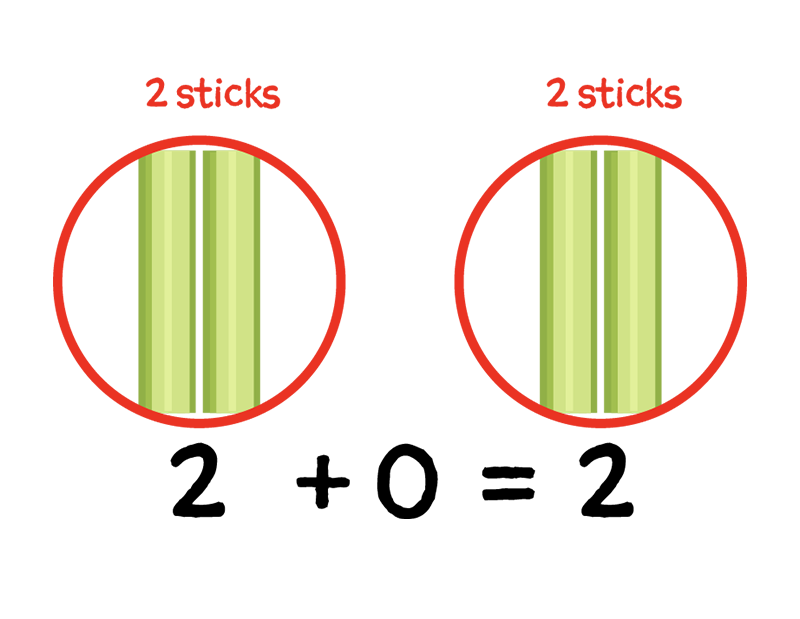
No, this is the identity property because we are adding 0 to a number.
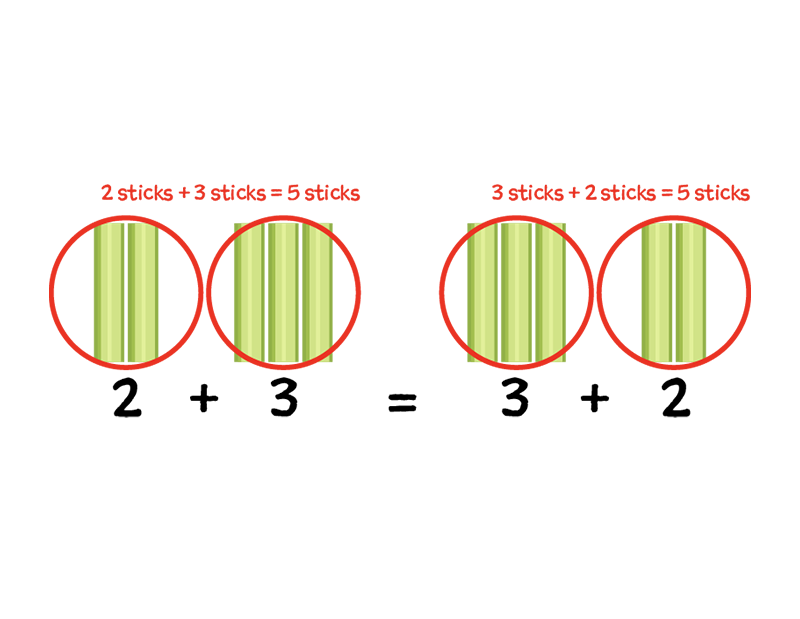
No, this is the commutative property because the addends switch places.
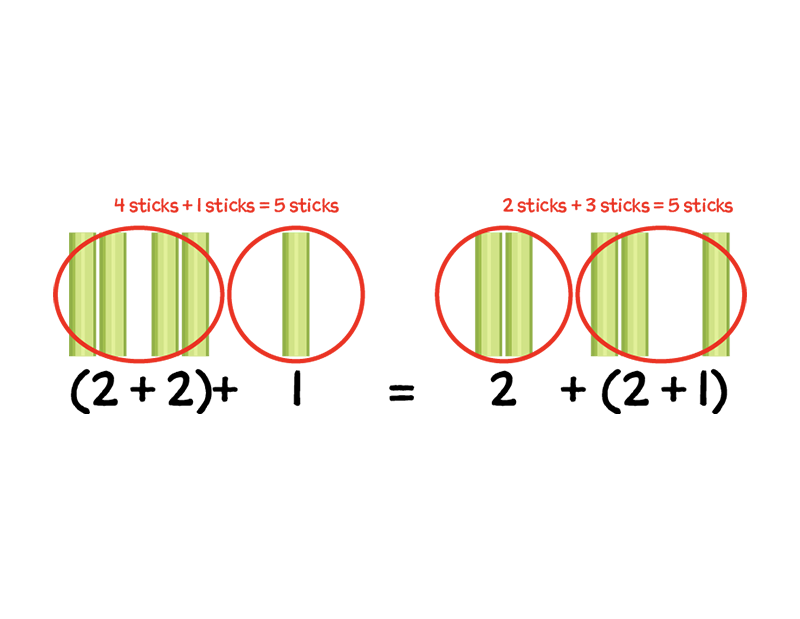
Yes, this is the associative property because we are adding the addends in different orders.
No, this is the distributive property because we add the numbers in parentheses first and then multiply.
Summary
Questions answered correctly:
Questions answered incorrectly:
How can we use the properties of operations to solve addition equations? The properties help us understand numbers and how they work together when we add or multiply. We can use what we have learned from each property to solve other addition equations.
Click each row to solve addition equations using the properties of operations.
|
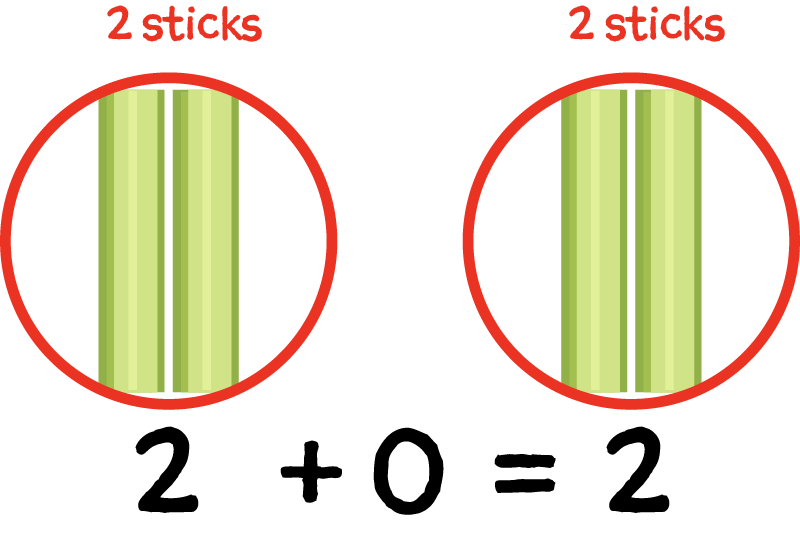
64+0=? We know that any number plus 0 is the same number. This is the identity property. 64 plus 0 equals 64. |
|
|
23+41=64
We know that changing the order of the addends does not change the sum. This is the commutative property. If 23 plus 41 equals 64, so does 41 plus 23 |
|
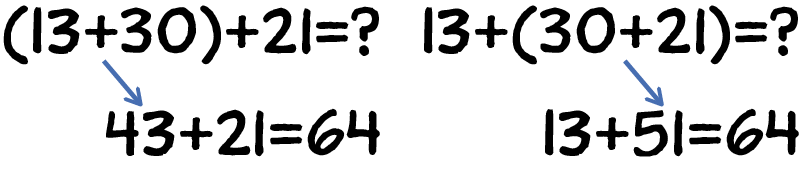
13+(30+21)=? arrow pointing to 43+21=64 or 13+(30+21)=? arrow point to 13+51=64 We know that we can add the addends in any order that works for us. This is the associative property. We can put parentheses around the two addends we want to add first. Both addition sentences equal 64. |
|
|
8×(4+4=?) arrow pointing to 8times(8)=64 This is the distributive property. We distribute the 8 by multiplying it by the first 4, then the second 4 and add the products together. |
Let’s use the properties of operations to solve Daniel’s math sentence!
We can use what we know about the properties of operations to solve addition and multiplication equations!