Let’s Learn!
Do you see equivalent fractions?
Goal:
Goal:
Zoe’s dad told her that the cars on her trains show equivalent fractions. Let’s look at them a little closer!
Question:
How can we tell if these fractions are equivalent?
Top: Toy train carrying a rectangle partitioned into 3 equal parts with 2 parts filled in.
Bottom: Toy train carrying a rectangle partitioned into 6 equal parts with 4 parts filled in.
We can see that the green takes up the same amount of space on both!
Top: Toy train carrying a rectangle partitioned into 3 equal parts with 2 parts filled in.
Bottom: Toy train carrying a rectangle partitioned into 6 equal parts with 4 parts filled in.
Top: Toy train carrying a rectangle partitioned into 3 equal parts with 2 parts filled in. \({ \frac{2}{3} }\)
Bottom: Toy train carrying a rectangle partitioned into 6 equal parts with 4 parts filled in. \({ \frac{4}{6} }\)
Equivalent fractions are two or more fractions that name the same amount using different fractions. For fractions to be equivalent, the shapes being compared must be the same size and shape. Both of the train cars are the same size and shape so we can compare! The first train shows \({ \frac{2}{3} }\) because 2 out of the 3 parts are green. The second train shows \({ \frac{4}{6} }\) because 4 out of the 6 parts are green. Even though these fractions are made up of different numbers, the same amount of each train car is green. \({ \frac{2}{3} }\) and \({ \frac{4}{6} }\) name the same amount, so they are equivalent!
Are these fractions equivalent? Click the squares to find out!
Top: Rectangle partitioned into 4 equal parts with 2 filled in. \({ \frac{2}{4} }\)
Bottom: Rectangle partitioned into 3 equal parts 2 filled in. \({ \frac{2}{3} }\)
Top: Rectangle partitioned into 4 equal parts with 2 filled in. \({ \frac{2}{4} }\)
Bottom: Rectangle partitioned into 3 equal parts 2 filled in. \({ \frac{2}{3} }\)
No! These fractions are not equivalent because the squares have different amounts of blue. \({ \frac{2}{3} }\) has more blue than \({ \frac{2}{4} }\), so they are not equivalent.
We can also look at \({ \frac{2}{3} }\) and \({ \frac{2}{4} }\) on a number line. Just like shapes, number lines must have the same lengths between 0 and 1 to use to compare. Do you see how the fractions do not quite line up? That is because they are not equivalent!
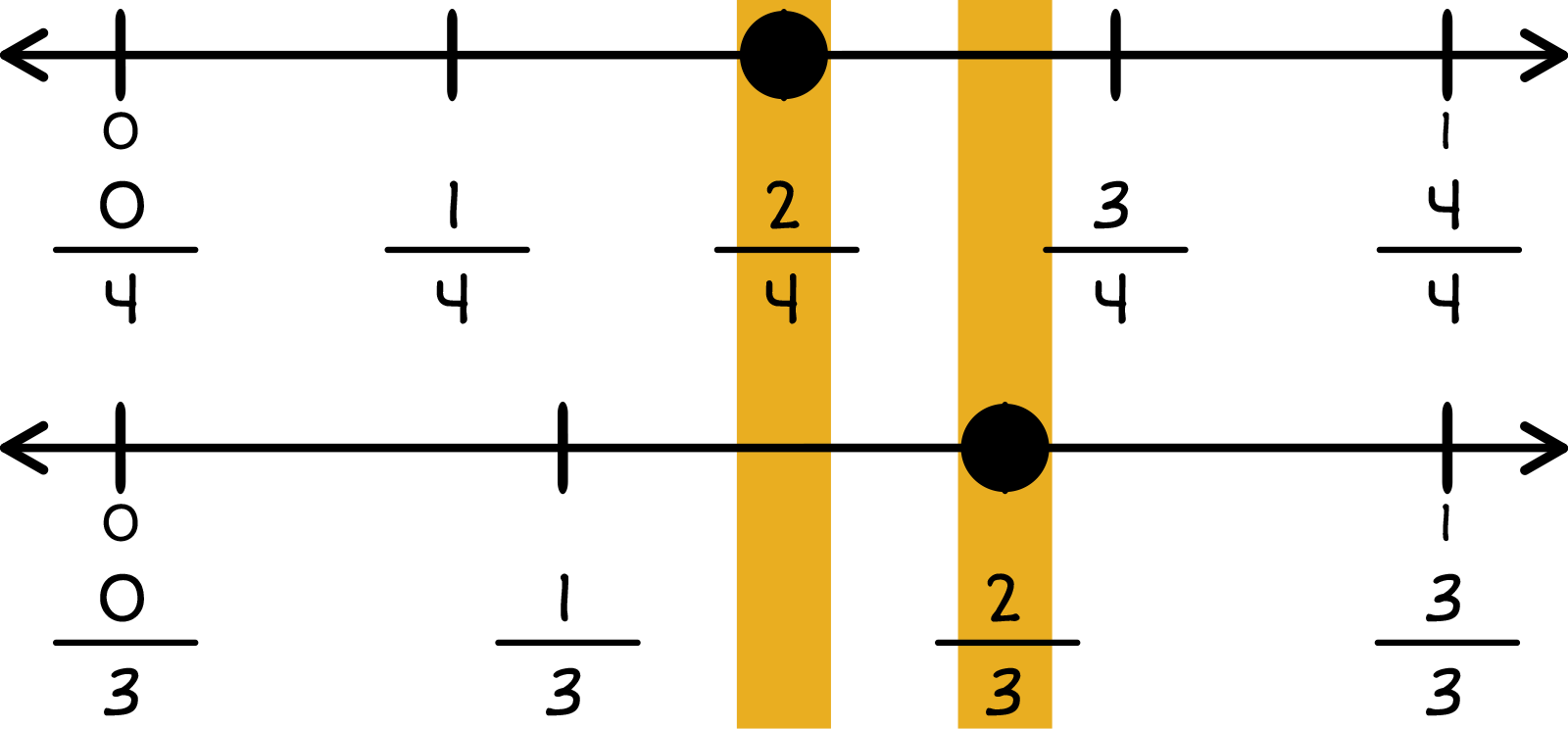
Top: Number line from 0 to 1 with 5 markers labeled from \({ \frac{0}{4} }\) to \({ \frac{4}{4} }\). Dot above \({ \frac{2}{4} }\).
Bottom: Number line from 0 to 1 with 5 markers labeled from \({ \frac{0}{3} }\) to \({ \frac{3}{3} }\). Dot above \({ \frac{2}{3} }\).
Top: Toy train carrying a rectangle partitioned into 3 equal parts with 2 parts filled in. \({ \frac{2}{3} }\)
Bottom: Toy train carrying a rectangle partitioned into 6 equal parts with 4 parts filled in. \({ \frac{4}{6} }\)
Do you remember Zoe’s train cars? Let’s look at \({ \frac{2}{3} }\) and \({ \frac{4}{6} }\) on a number line!
Top: Number line from 0 to 1 with 4 markers labeled from \({ \frac{0}{3} }\) to \({ \frac{3}{3} }\). Dot above \({ \frac{2}{3} }\).
Bottom: Number line from 0 to 1 with 7 markers labeled from \({ \frac{0}{6} }\) to \({ \frac{6}{6} }\). Dot above \({ \frac{4}{6} }\).
We said before that \({ \frac{2}{3} }\) and \({ \frac{4}{6} }\) are equivalent fractions. Let’s use number lines to be certain. Click the number lines to check.
Top: Number line from 0 to 1 with 4 markers labeled from \({ \frac{0}{3} }\) to \({ \frac{3}{3} }\). Dot above \({ \frac{2}{3} }\).
Bottom: Number line from 0 to 1 with 7 markers labeled from \({ \frac{0}{6} }\) to \({ \frac{6}{6} }\). Dot above \({ \frac{4}{6} }\).
Yes! \({ \frac{2}{3} }\) and \({ \frac{4}{6} }\) are equivalent fractions because the dots on both number lines line up!
Question:
How do you know if there are equivalent fractions on a number line?
The dots on both number lines line up!