Loading...

What are applications of trigonometric functions that can be graphed?

As you saw in the video, you can solve a trigonometric function for a specific value using technology. The instructor in the video show you how to solve for a specific value using a straight line and finding the points of intersection. Let’s walk through another example. Remember the Ferris wheel from the beginning of the lesson?

The height off the ground (y) in feet of the #1 car can be represented by the function \( y = 18\sin{\left( 0.2\left( x - 5 \right) \right) +}20 \), with time in x seconds. When does the #1 car on the Ferris wheel reach a height of 36 feet during the 3-minute ride? How many full circles does the Ferris wheel complete during that 3-minute ride?

Ferris wheel

For this problem, we need to figure out what to find and determine the viewing window to use. Since the ride takes 3 minutes and the x-axis is in seconds, we need to view at least from 0 to 180 along the x-axis. On the y-axis, look at the equation to determine that the amplitude is 18 and that it is shifting up 20 units—thus the graph will go up to 38 on the y-axis. Set the view window to at least 0 to 38.

What does the graph look like?

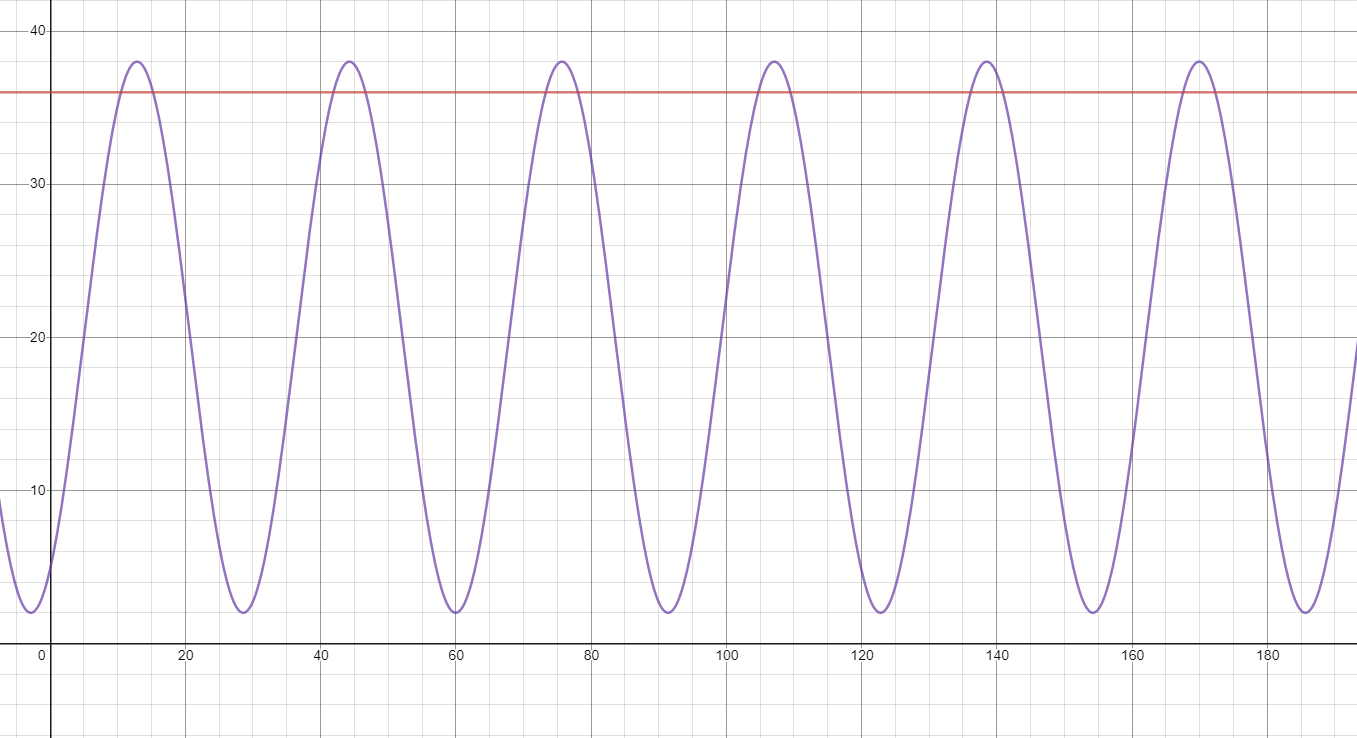
Next, you need to plot the line y = 36 because you are looking for the times when the height is 36. Finally, find the points of intersection between the original trigonometric function and the line. Those will be the times when the Ferris wheel is at 36 feet.

At what times will the #1 car be 36 feet above the ground?

Notice from the graph that the function makes about six complete cycles during the 180 seconds; thus, the Ferris wheel will rotate 6 times during the 3-minute ride.

Practice this process a few more times. For each situation, find when the Ferris wheel reaches a height of 40 feet.

The height of a Ferris wheel can be represented by the function \( y = - 20\cos{\left( \frac{\pi}{10}\left( x - 3 \right) \right) +}40 \) with time in \( x \) seconds on the interval \( 0 < x < 20 \).

The height of a Ferris wheel can be represented by the function \( y = 20\sin{\left( \frac{\pi}{6}\left( x - 6 \right) \right) +}24 \) with time in \( x \) seconds on the interval \( 0 < x < 20 \).

The height of a Ferris wheel can be represented by the function \( y = - 25\cos{\left( \frac{\pi}{12}\left( x - 4 \right) \right) +}30 \) with time in \( x \) seconds on the interval \( 0 < x < 20 \).