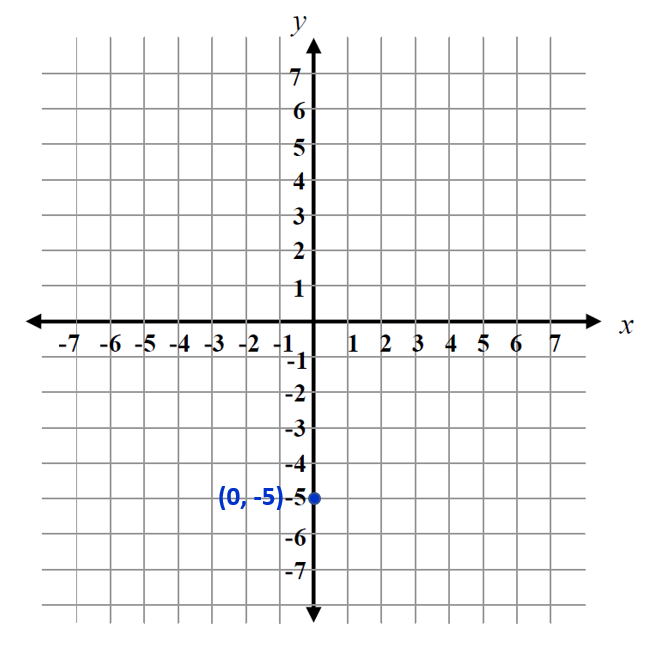
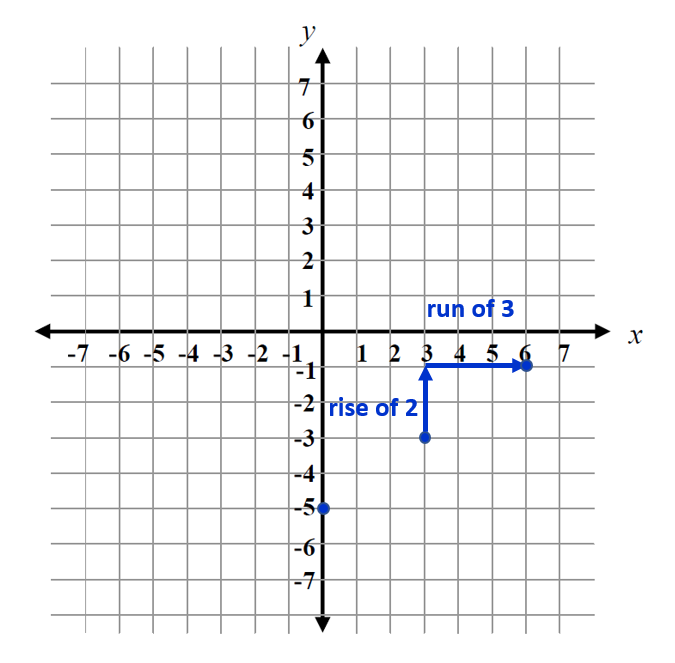
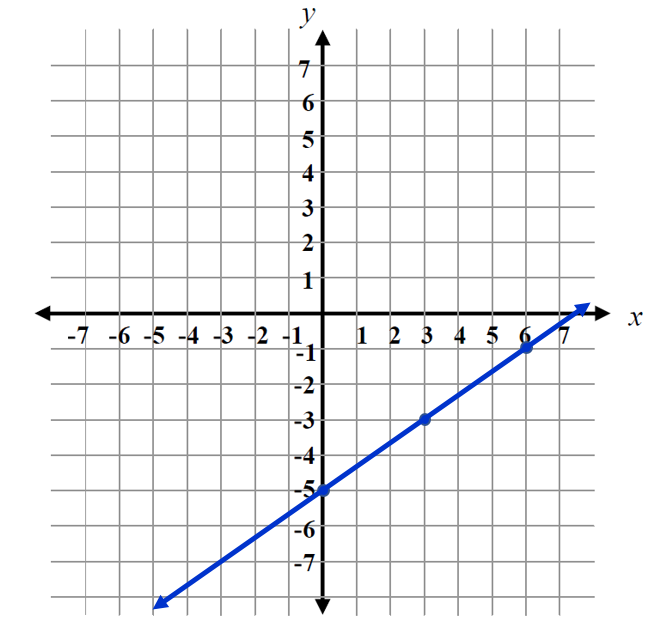
Graphing the line that represents an equation in slope-intercept form is a simple process. Let's look at the process for graphing the equation \(\mathsf{y = \frac{2}{3}x - 5 }\).
|
Step 1 Identify the y-intercept of the equation and plot a point at the intercept. b = -5
Step 2 Identify the slope and write it in fractional form to represent \(\mathsf{ \large\frac{rise}{run} }\). Put a whole number or integer over one. slope = \(\mathsf{ \large\frac{2}{3} }\)
Step 3 Starting with the intercept, move up or down according to the rise, then to right according to the run and plot another point. If the slope is negative, make the rise negative, meaning you move down instead of up.
Step 4 Starting with the new point, move up or down according to the rise, then to the right according to the run and plot another point.
Step 5 Draw a line through the points on the graph. You have now graphed the equation \(\mathsf{y = \frac{2}{3}x - 5 }\).
|