Ted decides he'd better practice a little before he tries to find the area of the community pool to make sure he remembers the process correctly. After all, he doesn't want to mess up his very first task as pool supervisor!
In the pool office, Ted finds a catalog with pictures of different pools for sale. Next to each pool is listed its area in square feet. See if you can do as well as Ted did with calculating area by applying the steps below.
| Divide the unknown figure into known figures. |
| Find the areas of the known figures using formulas you already know. |
| Sum the areas of the known figures in order to get the total area. |
First, figure out the area of each pool diagram. Then, connect the diagram to its correct area measurement.
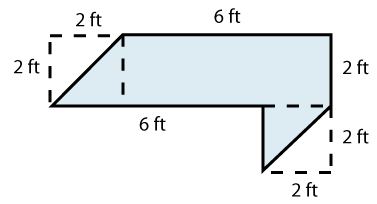 |
36 feet squared
16 feet squared
|
The dimensions of the rectangle are 6 feet by 2 feet, so the total area is 12 feet squared. The base and height of each triangle are two feet, so the area of each triangle is 2 feet multiplied by two feet divided by 2, or 2 feet squared. The total area of the shape is 12 feet squared plus 2 feet squared plus 2 feet squared, or 16 feet squared.
The dimensions of the rectangle are 6 feet by 2 feet, so the total area is 12 feet squared. The base and height of each triangle are two feet, so the area of each triangle is 2 feet multiplied by two feet divided by 2, or 2 feet squared. The total area of the shape is 12 feet squared plus 2 feet squared plus 2 feet squared, or 16 feet squared.
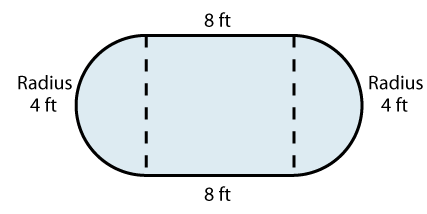 |
32 + 16π feet squared
64 + 16π feet squared
|
The area of the rectangle is 8 feet multiplied by 8 feet, which is 64 feet squared. The area of each half circle is π multiplied by 4 feet squared and then divided by 2 (since they are half circles), so 8π . When we add everything together, we get 64 + 16π feet squared.
The area of the rectangle is 8 feet multiplied by 8 feet, which is 64 feet squared. The area of each half circle is π multiplied by 4 feet squared and then divided by 2 (since they are half circles), so 8π . When we add everything together, we get 64 + 16π feet squared.
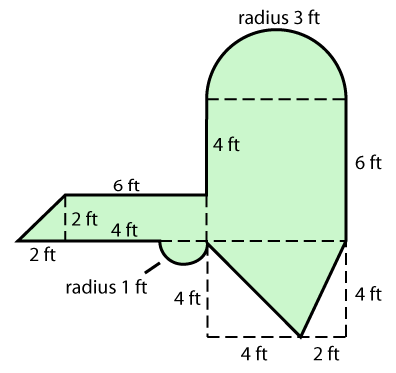 |
62 + 5π feet squared
80 + 12π feet squared
|
From left to right, the areas are: the triangle is 2 feet squared, the rectangle is 12 feet squared, the little half circle is .5π feet squared, the larger triangle is 12 feet squared, the square is 36 feet squared, and the large half circle is 4.5π feet squared. When you sum all of these together, you get 62 + 5π feet squared.
From left to right, the areas are: the triangle is 2 feet squared, the rectangle is 12 feet squared, the little half circle is .5π feet squared, the larger triangle is 12 feet squared, the square is 36 feet squared, and the large half circle is 4.5π feet squared. When you sum all of these together, you get 62 + 5π feet squared.
Complete
